
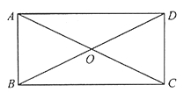
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
【答案】(1)证明见解析;(2)∠ADO==36°.
【解析】
(1)先判断四边形ABCD是平行四边形,继而根据已知条件推导出AC=BD,然后根据对角线相等的平行四边形是矩形即可;
(2)设∠AOB=4x,∠ODC=3x,则∠OCD=∠ODC=3x.,在△ODC中,利用三角形内角和定理求出x的值,继而求得∠ODC的度数,由此即可求得答案.
(1)∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形,
又∵∠AOB=2∠OAD,∠AOB是△AOD的外角,
∴∠AOB=∠OAD+∠ADO.
∴∠OAD=∠ADO.
∴AO=OD.
又∵AC=AO+OC=2AO,BD=BO+OD=2OD,
∴AC=BD.
∴四边形ABCD是矩形.
(2)设∠AOB=4x,∠ODC=3x,则∠ODC=∠OCD=3x,
在△ODC中,∠DOC+∠OCD+∠CDO=180°
∴4x+3x+3x=180°,解得x=18°,
∴∠ODC=3×18°=54°,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠ADO=∠ADC-∠ODC=90°-54°=36°.


科目:初中数学 来源: 题型:
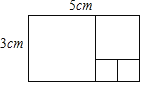
【题目】请将宽为3cm、长为ncm的长方形(n为正整数)分割成若干小正方形,要求小正方形的边长是正整数且个数最少.例如,当n=5cm时,此长方形可分割成如右图的4个小正方形.
请回答下列问题:
(1)n=16时,可分割成几个小正方形?
(2)当长方形被分割成20个小正方形时,求n所有可能的值;
(3)一般地,n>3时,此长方形可分割成多少个小正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
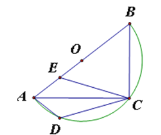
【题目】如图,在Rt△ABC中,∠ACB=90°,以AB为直径作半圆.点D在弧![]() 上(不与A,C重合),点E在AB上,且点D.E关于AC对称. 给出下列结论:①若∠ACE=20°,则∠BAC=25°;②若BC=3,AC=4,则
上(不与A,C重合),点E在AB上,且点D.E关于AC对称. 给出下列结论:①若∠ACE=20°,则∠BAC=25°;②若BC=3,AC=4,则![]() ;给出下列判断,正确的是( )
;给出下列判断,正确的是( )
A.①②都对B.①②都错C.①对②错D.①错②对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:![]() ,则
,则![]() 是“和谐分式”.
是“和谐分式”.
(1)下列分式中,属于“和谐分式”的是_____(填序号);
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(2)将“和谐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() =_______(要写出变形过程);
=_______(要写出变形过程);
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
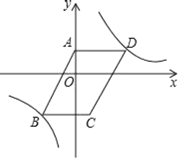
【题目】如图,在平面直角坐标系中,反比例函数y=![]() 经过ABCD的顶点B,D,点D的坐标为(2,1),点A在y轴上,且AD∥x轴,SABCD=6.
经过ABCD的顶点B,D,点D的坐标为(2,1),点A在y轴上,且AD∥x轴,SABCD=6.
(1)填空:点A的坐标为 ,k= ;
(2)求AB所在直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
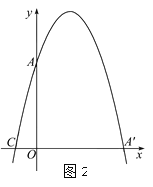
【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M时第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;
(3)若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)证明:无论m取何值,函数图象与x轴都有两个不相同的交点;
(2)当图象的对称轴为直线x=3时,求它与x轴两交点及顶点所构成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若抛物线![]() 与抛物线
与抛物线![]() 的开口大小相同,方向相反,且抛物线
的开口大小相同,方向相反,且抛物线![]() 经过
经过![]() 的顶点,我们称抛物线
的顶点,我们称抛物线![]() 为
为![]() 的“友好抛物线”.
的“友好抛物线”.
(1)若![]() 的表达式为
的表达式为![]() ,求
,求![]() 的“友好抛物线”的表达式;
的“友好抛物线”的表达式;
(2)已知抛物线![]() 为
为![]() 的“友好抛物线”.求证:抛物线
的“友好抛物线”.求证:抛物线![]() 也是
也是![]() 的“友好抛物线”;
的“友好抛物线”;
(3)平面上有点![]() ,
,![]() ,抛物线
,抛物线![]() 为
为![]() 的“友好抛物线”,且抛物线
的“友好抛物线”,且抛物线![]() 的顶点在第一象限,纵坐标为2,当抛物线
的顶点在第一象限,纵坐标为2,当抛物线![]() 与线段
与线段![]() 没有公共点时,求
没有公共点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列表格是某学校女子排球队队员年龄统计表:
年龄(岁) | 13 | 14 | 15 | 16 |
人数(人) | 1 | 2 | 4 | 5 |
(1)该排球队队员年龄的众数是 岁;
(2)事件“从该排球队随机选择一名队员,其年龄为13岁”发生的概率为 ;
(3)教练決定从年龄为13岁和14岁的A、B、C三名队员中,随机选取两名队员进行“接发球”训练,求队员A、B同时被选中的概率.(树状图或列表法)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com