
分析 (1)先移项,使方程的右边化为零,再将方程的左边分解为两个一次因式的乘积,然后令每个因式分别为零,得到两个一元一次方程,解这两个一元一次方程,它们的解就都是原方程的解;
(2)①当k=0时,是一元一次方程,有解;当k≠0时,方程是一元二次方程,因为方程有实数根,所以根据根的判别式△≥0,求出k的取值范围;
②当k=2时,把k值代入方程,用配方法解方程即可.
解答 解:(1)移项,得x(2x-6)-(x-3)=0,
分解因式,得(x-3)(2x-1)=0,
则x-3=0,或2x-1=0,
解得x1=3,x2=0.5;
(2)①当k=0时,方程可化为:2x-1=0,
解得,x=0.5.
当k≠0时,∵方程有实数根,
∴b2-4ac≥0,
即:4+4k≥0,
解得,k≥-1,
又∵k≠0,
∴k≥-1且k≠0,
综合上述可得,k≥-1;
②当k=2时,方程可化为2x2+2x=1,
二次项系数化为1,得x2+x=$\frac{1}{2}$,
配方得,(x+$\frac{1}{2}$)2=$\frac{3}{4}$,
解得,x=-$\frac{1}{2}$±$\frac{\sqrt{3}}{2}$,
即x1=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$,x2=-$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$.
点评 本题考查了根的判别式的运用,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
也考查了用因式分解法与配方法解方程.第二题第一问分两种情况讨论是解题的关键.


科目:初中数学 来源: 题型:填空题
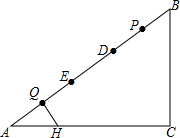 如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,点P,Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点E,D分别是点A,B以Q,P为对称中心的对称点,HQ⊥AB,垂足为点Q,交AC于点H.当点E到达顶点B时,Q,P同时停止运动,则当△HDE为等腰三角形时,BP的值为$\frac{40}{21}$或$\frac{40}{11}$或5或$\frac{320}{103}$.
如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,点P,Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点E,D分别是点A,B以Q,P为对称中心的对称点,HQ⊥AB,垂足为点Q,交AC于点H.当点E到达顶点B时,Q,P同时停止运动,则当△HDE为等腰三角形时,BP的值为$\frac{40}{21}$或$\frac{40}{11}$或5或$\frac{320}{103}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,点D,E分别是AC,AB上的两点,且$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{1}{2}$,若△ADE的面积为1cm2,则四边形EBCD的面积为( )cm2.
如图,在△ABC中,点D,E分别是AC,AB上的两点,且$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{1}{2}$,若△ADE的面积为1cm2,则四边形EBCD的面积为( )cm2.| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x-1}{{{x^2}-3x+2}}$ | B. | $\frac{1}{x+1}$ | C. | $\frac{2x-2}{x-2}$ | D. | $\frac{x+2}{x-1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com