
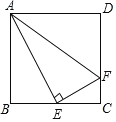
【题目】如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF.有下列结论:①∠BAE=30°;②射线FE是∠AFC的角平分线;③AE2=ADAF;④AF=AB+CF.其中正确结论为是______.(填写所有正确结论的序号)
【答案】②③④
【解析】
①根据题目中的条件和正方形的性质,利用锐角三角函数可以得到∠BAE是否等于30°;
②根据题目中的条件,可以求得∠AEB和∠CFE的正切值,从而可以得到射线FE是否为∠AFC的角平分线;
③由题中条件可得△CEF∽△BAE,进而得出对应线段成比例,进而又可得出△ABE∽△AEF,即可得出题中结论;
④根据题目中的条件和全等三角形的判定与性质,可以得到AF=AB+CF是否成立.
解:∵在正方形ABCD中,E是BC的中点,∠B=∠C=90°,
∴AB=BC,BE=![]() AB,
AB,
∴tan∠BAE=![]() =
=![]() ,
,
∵tan30°=![]() ,
,
∴∠BAE≠30°,故①错误;
∵∠B=∠C=90°,AE⊥EF,
∴∠BAE+∠BEA=90°,∠BEA+∠CEF=90°,∠CFE+∠CEF=90°,
∴∠BAE=∠CEF,∠BEA=∠CFE,
∴△ABE∽△ECF,
∴![]()
∵AB=2BE=2CE,
∴EC=2CF,
设CF=a,则EC=BE=2a,AB=4a,
∴在Rt△ABE中,AE=![]() a,
a,
在Rt△CEF中,EF=![]() a,tan∠CFE=2,
a,tan∠CFE=2,
∴tan∠AFE=![]() =2,
=2,
∴∠AFE=∠CFE,
即射线FE是∠AFC的角平分线,故②正确;
∵∠AFE=∠CFE,∠AEF=∠C,
∴∠EAF=∠CEF,
∵∠BAE=∠CEF,
∴∠BAE=∠EAF,
∴△ABE∽△AEF,
∴![]() ,
,
∴AE2=ABAF,
∵AD=AB,
∴AE2=ADAF,故③正确;
作EG⊥AF于点G,
∵FE平分∠AFC,∠C=90°,
∴EG=EC,
∴EG=EB,
∵∠B=∠AGE=90°,
在Rt△ABE和Rt△AGE中
![]()
∴Rt△ABE≌Rt△AGE(HL)
∴AB=AG,
又∵CF=GF,AF=AG+GF,
∴AF=AB+CF,故④正确,
由上可得,②③④正确,
故答案为:②③④.



科目:初中数学 来源: 题型:
【题目】第36届全国信息学冬令营在广州落下帷幕,长郡师生闪耀各大赛场,金牌数、奖牌数均稳居湖南省第一.学校拟预算7700元全部用于购买甲、乙、丙三种图书共20套奖励获奖师生,其中甲种图书每套500元,乙种图书每套400元,丙种图书每套250元,设购买甲种图书x套,乙种图书y套,请解答下列问题:
(1)请求出y与x的函数关系式(不需要写出自变量的取值范围);
(2)若学校购买的甲、乙两种图书共14套,求甲、乙图书各多少套?
(3)若学校购买的甲、乙两种图书均不少于1套,则有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把八个完全相同的小球平分为两组,每组中每个分别写上1,2,3,4四个数字,然后分别装入不透明的口袋内搅匀,从第一个口袋内取出一个数记下数字后作为点P的横坐标x,然后再从第二个口袋中取出一个球记下数字后作为点P的纵坐标,则点P(x,y)落在直线y=﹣x+5上的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
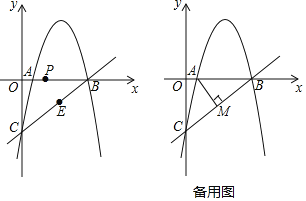
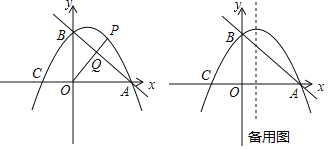
【题目】如图,抛物线![]() 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为
经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为![]() .
.
①求抛物线的解析式.
②点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.
③过点A作![]() 于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
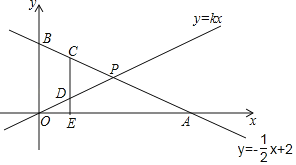
【题目】在平面直角坐标系中,一次函数y=﹣![]() x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P.
x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P.
(1)求点A、B的坐标;
(2)若OP=PA,求k的值;
(3)在(2)的条件下,C是线段BP上一点,CE⊥x轴于E,交OP于D,若CD=2ED,求C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数y=![]() (x>0)的图象与直线y=
(x>0)的图象与直线y=![]() x+1交于点A(2,m).
x+1交于点A(2,m).
(1)求k、m的值;
(2)已知点P(n,0),过点P作平行于 y 轴的直线,交直线y=![]() x+1于点B,交函数y=
x+1于点B,交函数y=![]() (x>0)的图象于点C.若y=
(x>0)的图象于点C.若y=![]() (x>0)的图象在点A、C之间的部分与线段AB、BC所围成的区域内(不包括边界),记作图形G.横、纵坐标都是整数的点叫做整点.
(x>0)的图象在点A、C之间的部分与线段AB、BC所围成的区域内(不包括边界),记作图形G.横、纵坐标都是整数的点叫做整点.
①当n=4时,直接写出图形G的整点坐标;
②若图形G 恰有2 个整点,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
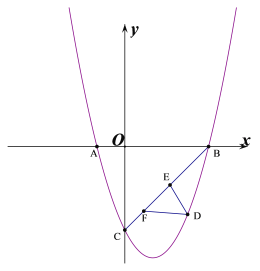
【题目】如图所示,抛物线y=ax2+bx-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)求抛物线的解析式.
(2)如图,直线BC下方的抛物线上有一点D,过点D作DE⊥BC于点E,作DF平行x轴交直线BC于点F,求△DEF周长的最大值.
(3)已知点M是抛物线的顶点,点N是y轴上一点,点Q是坐标平面内一点,若点P是抛物线上一点,且位于抛物线对称轴的右侧,是否存在以点P,M,N,Q为顶点且以PM为边的正方形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+3与x轴交于点A,与y轴交于点B.抛物线y=﹣
x+3与x轴交于点A,与y轴交于点B.抛物线y=﹣![]() x2+bx+c经过A、B两点,与x轴的另一个交点为C.
x2+bx+c经过A、B两点,与x轴的另一个交点为C.
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的点,连接OP交直线AB于点Q.设点P的横坐标为m,PQ与OQ的比值为y,求y与m的关系式,并求出PQ与OQ的比值的最大值;
(3)点D是抛物线对称轴上的一动点,连接OD、CD,设△ODC外接圆的圆心为M,当sin∠ODC的值最大时,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com