
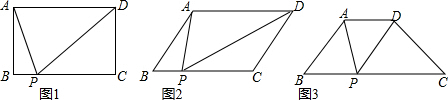
���� ��1�����ı���ABCD�Ǿ��Σ��õ���B=��C=90�㣬������ǵ����ʵõ���BAP=��DPC���Ƴ���ABP�ס�PCD���������������ε����ʼ��ɵõ����ۣ�
��2���ӳ�BC����E��ʹ��CD��DE��ͨ����ABP�ס�DPE���з��̵õ�BP=1������P��PF��AB����ֱ�������μ��ɵõ����ۣ�
��3����AE��BC��DF��BC���õ���AEP=��DFP=90�㣬�Ƴ���AEP�ס�PFD���������������ε����ʵõ�AE•DF=PE•PF=4����PE+PF��2$\sqrt{PE•PF}$�����ɵõ����ۣ�
��� �⣺��1�����ı���ABCD�Ǿ��Σ�
���B=��C=90�㣬
�ߡ�APD=��B=90�㣬
���PAB+��APB=��APB+��DPC=90�㣬
���BAP=��DPC��
���ABP�ס�PCD��
��$\frac{AB}{BP}=\frac{PC}{CD}$��
��BP=x����$\frac{4}{x}=\frac{10-x}{4}$
��x1=2��x2=8����BP��PC��
��BP=2��
��2���ӳ�BC����E��ʹ��CD��DE��
��AB=2$\sqrt{2}$��BC=5����APD=��B=45�㣬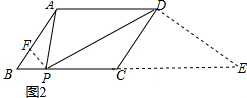
���DPE=��BAP����B=��E=45�㣬
���ABP�ס�DEP��
��$\frac{AB}{BP}=\frac{PE}{DE}$��
��BP=x��CE=$\sqrt{2}$CD=4��
��$\frac{{2\sqrt{2}}}{x}=\frac{9-x}{{2\sqrt{2}}}$��
��BP=1��
����P��PF��AB��
��BF=PF=$\frac{\sqrt{2}}{2}$��AF=$\frac{3\sqrt{2}}{2}$��
��AP=$\sqrt{5}$��
��3��AD��4��
��AE��BC��DF��BC��
���AEP=��DFP=90�㣬
�ߡ�APD=90�㣬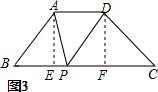
���EAP+��APE=��APE+��DPF=90�㣬
���EAP=��DPF��
���AEP�ס�PFD��
��$\frac{AE}{PE}=\frac{PF}{DF}$��
��AE•DF=PE•PF=4��
��PE+PF��2$\sqrt{PE•PF}$��
��AD=PE+PF��4��
�ʴ�Ϊ��AD��4��
���� ���⿼���˾��ε����ʣ�ƽ���ı��ε����ʣ����ε����ʣ����������ε��ж������ʣ���ȷ�����������߹��������������ǽ���Ĺؼ���


 ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
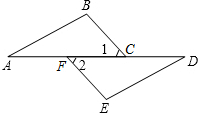 ��ͼ����֪����A=��D����1=��2��������������ʹ��ABC�ա�DEF���ǣ�������
��ͼ����֪����A=��D����1=��2��������������ʹ��ABC�ա�DEF���ǣ�������| A�� | ��E=��B | B�� | ED=BC | C�� | AB=EF | D�� | AF=CD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
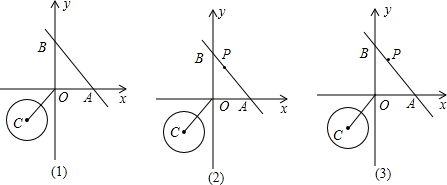
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
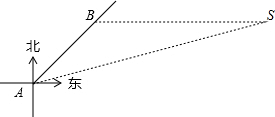 ��ͼ��һ���������еĴ�����A���۲����S�ڴ��ı�ƫ��67.5��ķ�����6�����B������ʱ����Sǡ���ڴ�������������֪����˵���8��������ĺ���Ϊ���а�ȫ�������Ҵ����Լ����ض�����������Ϊʲô�����ο����ݣ�tan22.5���$\frac{2}{5}$��sin22.5���$\frac{19}{50}$��cos22.5���$\frac{23}{25}$��
��ͼ��һ���������еĴ�����A���۲����S�ڴ��ı�ƫ��67.5��ķ�����6�����B������ʱ����Sǡ���ڴ�������������֪����˵���8��������ĺ���Ϊ���а�ȫ�������Ҵ����Լ����ض�����������Ϊʲô�����ο����ݣ�tan22.5���$\frac{2}{5}$��sin22.5���$\frac{19}{50}$��cos22.5���$\frac{23}{25}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com