
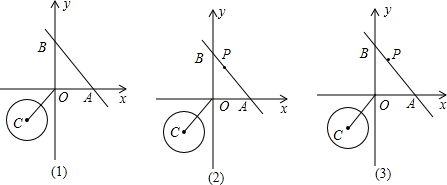
分析 (1)先求得直线OC的解析式,依据一次项系数乘积为-1的两条直线相互垂直,可证明CG⊥AB;
(2)由y=x与y=-x+2可求得点G的坐标,然后再求得点B的坐标为,接下来依据两点间的距离公式求得OC=2$\sqrt{2}$,OG=$\sqrt{2}$.BG=$\sqrt{2}$.接下来证明△OCE∽△OPG,由相似三角形的性质可求得PG=$\frac{\sqrt{6}}{3}$,从而可求得BP的长,故此可求得t的值
(3)如图所示:先证明△MOC∽△GOP,由相似三角形的性质可得到y与x的函数关系式,当点P与点G重合时,OP有最小值,当OP与圆C相切时OP有最大值,从而可确定出自变量x的取值范围.
解答 解:(1)∵设直线OC的解析式为y=kx,将点C的坐标代入得:-2k=-2,解得;k=1,
∴直线OC的解析式为y=x.
∵函数y=-x+2的一次项系数与函数y=x的一次项系数的乘积为-1×1=-1,
∴直线y=x与直线y=-x+2相互垂直.
∴CG⊥AB.
(2)∵将y=x与y=-x+2联立解得:x=1,y=1,
∴点G坐标为(1,1).
∵将x=0代入y=-x+2得y=2,
∴点B的坐标为(0,2).
由两点间的距离公式可知OC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,OG=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$.BG=$\sqrt{{(1-0)}^{2}+(2-1)^{2}}$=$\sqrt{2}$.
①如图1所示:
∵直线PO与⊙C相切,
∴CE⊥OE.
在Rt△OCE中,由勾股定理可知:OE=$\sqrt{O{C}^{2}-E{C}^{2}}$=$\sqrt{6}$
∵在△OCE和△OGP中,∠CEO=∠PGO=90°,∠COE=∠POG,
∴△OCE∽△OPG.
∴$\frac{CE}{PG}=\frac{OE}{OG}$,即$\frac{\sqrt{2}}{PG}=\frac{\sqrt{6}}{\sqrt{2}}$,解得:PG=$\frac{\sqrt{6}}{3}$.
∴PB=BG-PG=$\sqrt{2}$-$\frac{\sqrt{6}}{3}$.
∴t=$\sqrt{2}$-$\frac{\sqrt{6}}{3}$.
②如图2所示:
∵直线PO与⊙C相切,
∴CE⊥OE.
在Rt△OCE中,由勾股定理可知:OE=$\sqrt{O{C}^{2}-E{C}^{2}}$=$\sqrt{6}$
∵在△OCE和△OGP中,∠CEO=∠PGO=90°,∠COE=∠POG,
∴△OCE∽△OPG.
∴$\frac{CE}{PG}=\frac{OE}{OG}$,即$\frac{\sqrt{2}}{PG}=\frac{\sqrt{6}}{\sqrt{2}}$,解得:PG=$\frac{\sqrt{6}}{3}$.
∴PB=BG+PG=$\sqrt{2}$+$\frac{\sqrt{6}}{3}$.
∴t=$\sqrt{2}$+$\frac{\sqrt{6}}{3}$.
综上所述,当t=$\sqrt{2}$+$\frac{\sqrt{6}}{3}$或t=$\sqrt{2}$-$\frac{\sqrt{6}}{3}$时,直线PO与⊙C相切.
(3)如图所示:
∵CM⊥EF,
∴∠CMO=90°.
∴∠CMO=∠OGP.
又∵∠MOC=∠GOP,
∴△MOC∽△GOP.
∴$\frac{OC}{OP}=\frac{OM}{OG}$,即$\frac{2\sqrt{2}}{x}=\frac{y}{\sqrt{2}}$.
∴xy=4.
∴y与x的函数关系式为y=$\frac{4}{x}$.
∵当直线OP与圆C相切时,x有最大值,
∴OP=$\sqrt{(\sqrt{2})^{2}+(\frac{\sqrt{6}}{3})}$=$\frac{2\sqrt{6}}{3}$.
当点P与点G重合时,x有最小值,最小值=OG=$\sqrt{2}$.
∴自变量x的取值范围是$\sqrt{2}$≤x≤$\frac{2\sqrt{6}}{3}$.
点评 本题主要考查的是圆的综合应用,解答本题主要应用了切线的性质、相似三角形的性质和判定、勾股定理、待定系数法求一次函数的解析式,证得△OCE∽△OPG、△MOC∽△GOP是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.45×108 | B. | 14.5×108 | C. | 1.45×109 | D. | 14.5×109 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com