
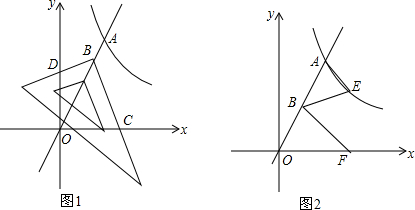
���� ��1���Ȱ�A��3��n������y=2x���n���Ӷ��õ�A��3��6���������������ľ��빫ʽ�����OA=3$\sqrt{5}$��Ȼ����ݷ���������ͼ���ϵ������������m=18��
��2����B�ֱ���x���y��Ĵ��ߣ�����ֱ�ΪM��N����ͼ1����B��a��2a������BM=2a��BN=a�����õȽǵ������ȵõ���MBC=��DBN�����ǿ��ж�Rt��MBC��Rt��DBN��Ȼ���������Ʊ���$\frac{BC}{BD}$=2��
��3����AH��y����H���ӳ�AE��x����G�㣬����GB����ͼ2���ɡ�EAB=��AOF�õ���GAOΪ���������Σ��ٸ��ݵ��������ε����ʵ�GB��OA������֤��Rt��OBG��Rt��AHO���������Ʊȼ����OG=$\frac{15}{2}$���õ�G��$\frac{15}{2}$��0����Ȼ�����ô���ϵ�������ֱ��AG�Ľ���ʽΪy=-$\frac{4}{3}$x+10����ͨ���ⷽ����$\left\{\begin{array}{l}{y=\frac{18}{x}}\\{y=-\frac{4}{3}x+10}\end{array}\right.$��E������Ϊ��$\frac{9}{2}$��4�������ǿ����������ľ��빫ʽ�����AE=$\frac{5}{2}$�����֤����ABE�ס�OFB���������Ʊȼ����OF���Ӷ��õ�F������꣮
���  �⣺��1����A��3��n������y=2x��n=2��3=6����A��3��6����
�⣺��1����A��3��n������y=2x��n=2��3=6����A��3��6����
����OA=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$��
����A�ڷ���������y=$\frac{m}{x}$ͼ���ϣ�
����m=3��6=18��
�ʴ�Ϊ18��3$\sqrt{5}$��
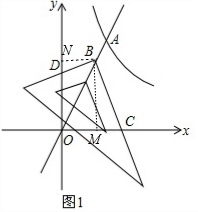
��2����B�ֱ���x���y��Ĵ��ߣ�����ֱ�ΪM��N����ͼ1����B��a��2a������BM=2a��BN=a��
�ߡ�MBC+��MBD=90�㣬��DBN+��MBD=90�㣬
���MBC=��DBN��
��Rt��MBC��Rt��DBN��
��$\frac{BC}{BD}$=$\frac{BM}{BN}$=$\frac{2a}{a}$=2��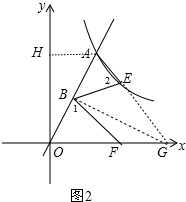 ��3�����ڣ�
��3�����ڣ�
��AH��y����H���ӳ�AE��x����G�㣬����GB����ͼ2��
�ߡ�EAB=��AOF��
���GAO����������
��B���߶�OA���е㣬
��GB��OA��
��AH��x�ᣬ
���OAH=��GOB��
��Rt��OBG��Rt��AHO��
��$\frac{OG}{OA}$=$\frac{OB}{AH}$����$\frac{OG}{3\sqrt{5}}$=$\frac{\frac{3\sqrt{5}}{2}}{3}$�����OG=$\frac{15}{2}$
��G��$\frac{15}{2}$��0����
��ֱ��AG�Ľ���ʽΪy=kx+b��
��A��3��6����G��$\frac{15}{2}$��0�������$\left\{\begin{array}{l}{3k+b=6}\\{\frac{15}{2}k+b=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=10}\end{array}\right.$��
��ֱ��AG�Ľ���ʽΪy=-$\frac{4}{3}$x+10��
�ⷽ����$\left\{\begin{array}{l}{y=\frac{18}{x}}\\{y=-\frac{4}{3}x+10}\end{array}\right.$��$\left\{\begin{array}{l}{x=3}\\{y=6}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{9}{2}}\\{y=4}\end{array}\right.$��
��E��������$\frac{9}{2}$��4����
��AE=$\sqrt{��3-\frac{9}{2}��^{2}+��6-4��^{2}}$=$\frac{5}{2}$��
�ߡ�EBO=��EAB+��2������1+��EBF=��EAB+��2��
����EAB=��EBF��
���1=��2��
�ߡ�EAB=��BOF��
���ABE�ס�OFB��
��$\frac{AB}{OF}$=$\frac{AE}{OB}$����$\frac{\frac{3\sqrt{5}}{2}}{OF}$=$\frac{\frac{5}{2}}{\frac{3\sqrt{5}}{2}}$��
��OF=$\frac{9}{2}$��
��F���������$\frac{9}{2}$��0����
���� ���⿼���˷����������ۺ��⣺�������շ���������ͼ���ϵ������������һ�κ���ͼ���ϵ����������������������ͼ�����ʣ������������ľ��빫ʽ�����߶εij������������������ε��ж������ʼ����߶εij��ȣ�


 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д� ����������������ϵ�д�
����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2•a3=a6 | B�� | 7a2-a2=7 | ||
| C�� | -$��-\frac{1}{2}��^{-2}$•��xy2��3=-4x3y6 | D�� | ��2m-n��2=4m2+n2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
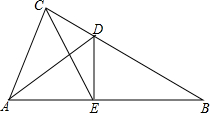 ��ͼ���ڡ�ABC�У���ACB=90�㣬ADƽ�֡�CAB����CB�ڵ�D������D��DE��AB������Ϊ��E��
��ͼ���ڡ�ABC�У���ACB=90�㣬ADƽ�֡�CAB����CB�ڵ�D������D��DE��AB������Ϊ��E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
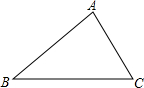 ��ͼ�����߾����ȳ�����ǡ�ABC�����ڴ�����������һ��O��ʹ�á�OAB����OBC����OCA���������ȣ�������������ȷ���ǣ�������
��ͼ�����߾����ȳ�����ǡ�ABC�����ڴ�����������һ��O��ʹ�á�OAB����OBC����OCA���������ȣ�������������ȷ���ǣ�������| A�� | ������AD����ȡAD���е�O | |
| B�� | �ֱ���AB��BC�ĸ��ߣ���ȡ�������ߵĽ���O | |
| C�� | �ֱ�������AD��BE����ȡ�������ߵĽ���O | |
| D�� | �ֱ�����A����B�Ľ�ƽ���ߣ���ȡ������ƽ���ߵĽ���O |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �ۼ�x��Ԫ/ǧ�ˣ� | �� | 50 | 60 | 70 | 80 | �� |
| ������y��ǧ�ˣ� | �� | 100 | 90 | 80 | 70 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3��2�� | B�� | ��-3��-2�� | C�� | ��2��-2�� | D�� | ��-1��6�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com