
分析 (1)根据一元二次方程的定义得k≠0,再计算判别式得到△=(2k-2)2-4k×(k-2)>0,然后根据非负数的性质即k的取值得到△>0,则可根据判别式的意义得到结论,;
(2)利用公式法表示出方程的两个根,再进一步理由方程有整数根探讨得出k的数值即可.
解答 (1)证明:这∵a=k,b=-(2k-2),c=k-2,
∴△=b2-4ac=[-(2k-2)]2-4k×(k-2)=4k2-8k+4-4k2+8k=4>0,
∴无论k取何值时,方程总有两个不相等的实数根.
(2)解:方程kx2-(2k-2)x+(k-2)=0(k≠0)的解为:$x=\frac{{-b±\sqrt{{b^2}-4ac}}}{2a}=\frac{{2k-2±\sqrt{4}}}{2k}$
整理,得${x_1}=1,{x_2}=\frac{k-2}{k}$
在方程的两个根中,x1=1是整数,
∴${x_2}=\frac{k-2}{k}$为整数,${x_2}=\frac{k-2}{k}=1-\frac{2}{k}$,
∵k为整数,
∴当k为±1和±2时方程有整数根.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.


科目:初中数学 来源: 题型:选择题
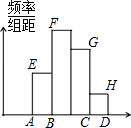 某校七年级在“数学小论文”评比活动中,共征集到论文30篇,并对其进行评比、整理,分成组画出频数分布直方图(如图),从左到右各小长方形的高度比为2:4:3:1,则第2组的频数为( )
某校七年级在“数学小论文”评比活动中,共征集到论文30篇,并对其进行评比、整理,分成组画出频数分布直方图(如图),从左到右各小长方形的高度比为2:4:3:1,则第2组的频数为( )| A. | 12 | B. | 10 | C. | 9 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 都有可能 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com