
分析 先把各二次根式化为最简二次根式,再移项合并得到a-12+(b-$\frac{1}{4}$)×$\sqrt{2}$=0,由于a,b为有理数,根据实数运算得到a-12=0,b-$\frac{1}{4}$=0,解得a=12,b=$\frac{1}{4}$,然后计算ab的值.
解答 解:∵$\sqrt{8}$×$\sqrt{18}$+$\sqrt{\frac{1}{8}}$=a+b$\sqrt{2}$,
∴2$\sqrt{2}$×3$\sqrt{2}$+$\frac{\sqrt{2}}{4}$=a+b$\sqrt{2}$,
∴12+$\frac{\sqrt{2}}{4}$=a+b$\sqrt{2}$,
∴a-12+(b-$\frac{1}{4}$)×$\sqrt{2}$=0,
∵a,b为有理数,
∴a-12=0,b-$\frac{1}{4}$=0,解得a=12,b=$\frac{1}{4}$,
∴ab=12×$\frac{1}{4}$=3.
故答案为3.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.


科目:初中数学 来源: 题型:解答题
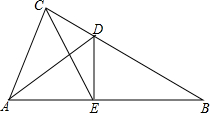 如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,垂足为点E.
如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
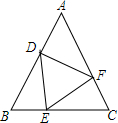 已知,如图,△ABC中,AB=AC,动点D、E、F在AB、BC、AC上移动,移动过程中始终保持BD=CE,∠DEF=∠B,请你分析是否存在始终与△BDE全等的三角形,并说明理由.
已知,如图,△ABC中,AB=AC,动点D、E、F在AB、BC、AC上移动,移动过程中始终保持BD=CE,∠DEF=∠B,请你分析是否存在始终与△BDE全等的三角形,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com