
【题目】如图,在边长为4的正方形ABCD中,对角线AC,BD相交于点O,点E是AD边上一点,连接CE,把△CDE沿CE翻折,得到△CPE,EP交AC于点F,CP交BD于点G,连接PO,若PO∥BC,则四边形OFPG的面积是 . 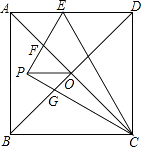
【答案】8﹣4 ![]()
【解析】解:如图所示,过P作PM⊥AO于M,作PN⊥BO于N,延长PO交CD于H,
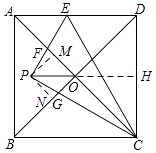
∵PO∥BC,BC⊥CD,
∴PH⊥CD,
又∵△CDO是等腰直角三角形,
∴OH= ![]() CD=2=CH,OH平分∠COD,
CD=2=CH,OH平分∠COD,
由折叠可得,CP=CD=4,
∴Rt△PCH中,PH= ![]() =2
=2 ![]() ,
,
∴PO=PH﹣OH=2 ![]() ﹣2,
﹣2,
∵PO平分∠AOB,PM⊥AO,PN⊥BO,
∴PM=PN,
矩形PMON是正方形,
∴正方形PMON的面积= ![]() OP2=
OP2= ![]() (2
(2 ![]() ﹣2)2=8﹣4
﹣2)2=8﹣4 ![]() ,
,
∵∠FPG=∠MON=90°,
∴∠FPM=∠GPN,
在△PMF和△PNG中,
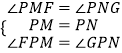 ,
,
∴△PMF≌△PNG(ASA),
∴S△PMF=S△PNG,
∴S四边形OFPG=S正方形PMON,
∴四边形OFPG的面积是8﹣4 ![]() ,
,
故答案为:8﹣4 ![]() .
.
通过做辅助线过P作PM⊥AO于M,作PN⊥BO于N,延长PO交CD于H,又因△CDO是等腰直角三角形,可得OH=2=CH,OH平分∠COD,由折叠的性质可得,CP=CD=4,有勾股定理可得PH =2 ![]() ,PO=PH﹣OH=2
,PO=PH﹣OH=2 ![]() ﹣2,得到正方形PMON的面积,得到△PMF≌△PNG(ASA),得到S△PMF=S△PNG,S四边形OFPG=S正方形PMON,求出四边形OFPG的面积是8﹣4
﹣2,得到正方形PMON的面积,得到△PMF≌△PNG(ASA),得到S△PMF=S△PNG,S四边形OFPG=S正方形PMON,求出四边形OFPG的面积是8﹣4 ![]() .
.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1,0),B(x2,0)(0<x1<x2)两点,与y轴交于点C.
(1)设AB=2,tan∠ABC=4,求该抛物线的解析式;
(2)在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;
(3)是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A | 0≤t≤0.5 | 6 | 0.15 |
B | 0.5≤t≤1 | a | 0.3 |
C | 1≤t≤1.5 | 10 | 0.25 |
D | 1.5≤t≤2 | 8 | b |
E | 2≤t≤2.5 | 4 | 0.1 |
合计 | 1 |
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() .
.
(1)如图1,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .若
.若![]() ,求证:
,求证:![]() ;
;
(2)如图2,![]() 是
是![]() 上的点,过点
上的点,过点![]() 作
作![]() ,交线段
,交线段![]() 于点
于点![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .若
.若![]() ,
,
①求证:![]() ;
;
②当![]() 时,求
时,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
把两个相同的数连接在一起就得到一个新数,我们把它称为“连接数”,例如:234234,3939…等,都是连接数,其中,234234称为六位连接数,3939称为四位连接数.
(1)请写出一个六位连接数 , 它(填“能”或“不能”)被13整除.
(2)是否任意六位连接数,都能被13整除,请说明理由.
(3)若一个四位连接数记为M,它的各位数字之和的3倍记为N,M﹣N的结果能被13整除,这样的四位连接数有几个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )
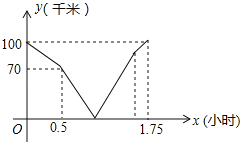
A. 乙先出发的时间为0.5小时 B. 甲的速度是80千米/小时
C. 甲出发0.5小时后两车相遇 D. 甲到B地比乙到A地早![]() 小时
小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com