
【题目】已知正方形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() .
.
(1)如图1,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .若
.若![]() ,求证:
,求证:![]() ;
;
(2)如图2,![]() 是
是![]() 上的点,过点
上的点,过点![]() 作
作![]() ,交线段
,交线段![]() 于点
于点![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .若
.若![]() ,
,
①求证:![]() ;
;
②当![]() 时,求
时,求![]() 的长.
的长.

【答案】(1)证明见解析(2)①证明见解析②![]()
【解析】
试题分析:(1)根据正方形的性质,可根据三角形全等的判定(ASA)与性质求证即可;
(2)①同(1)中,利用上面的结论,根据SAS可证的结论;
②设CH=x,然后根据正方形的性质和相似三角形的判定与性质可得![]() ,然后列方程求解即可.
,然后列方程求解即可.
试题解析:(1)证明:∵四边形ABCD是正方形
∴AC⊥BD,OD=OC
∴∠DOG=∠COE=90°
∴∠OEC+∠OCE=90°
∵DF⊥CE
∴∠OEC+∠ODG=90°
∴∠ODG=∠OCE
∴△DOG≌△COE(ASA)
∴OE=OG
(2)①证明:∵OD=OC,∠DOG=∠COE=90°
又OE=OG
∴△DOG≌△COE(SAS)
∴∠ODG=∠OCE
②解:设CH=x,
∵四边形ABCD是正方形,AB=1
∴BH=1-x
∠DBC=∠BDC=∠ACB=45°
∵EH⊥BC
∴∠BEH=∠EBH=45°
∴EH=BH=1-x
∵∠ODG=∠OCE
∴∠BDC-∠ODG=∠ACB-∠OCE
∴∠HDC=∠ECH
∵EH⊥BC
∴∠EHC=∠HCD=90°
∴△CHE∽△DCH
∴![]()
∴HC2=EH·CD
得x2+x-1=0
解得![]() ,
,![]() (舍去)
(舍去)
∴HC=![]()


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】【探究函数y=x+![]() 的图象与性质】
的图象与性质】
(1)函数y=x+![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下列四个函数图象中函数y=x+![]() 的图象大致是 ;
的图象大致是 ;
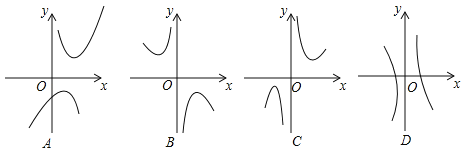
(3)对于函数y=x+![]() ,求当x>0时,y的取值范围.
,求当x>0时,y的取值范围.
请将下列的求解过程补充完整.
解:∵x>0
∴y=x+![]() =(
=(![]() )2+(
)2+(![]() )2=(
)2=(![]() ﹣
﹣![]() )2+
)2+
∵(![]() ﹣
﹣![]() )2≥0
)2≥0
∴y≥ .
[拓展运用]
(4)若函数y=![]() ,则y的取值范围 .
,则y的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=α(0°<α<60°),分别以AB、BC为边作等边三角形ABE和等边三角形BCD,连结CE,如图1所示.
(1)直接写出∠ABD的大小(用含α的式子表示);
(2)判断DC与CE的位置关系,并加以证明;
(3)在(2)的条件下,连结DE,如图2,若∠DEC=45°,求α的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
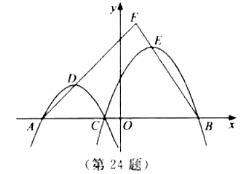
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一点(与
上一点(与![]() ,
,![]() 点不重合),抛物线
点不重合),抛物线![]()
![]() (
(![]() )经过点
)经过点![]() ,
,![]() ,顶点为
,顶点为![]() ,抛物线
,抛物线![]()
![]() (
(![]() )经过点
)经过点![]() ,
,![]() ,顶点为
,顶点为![]() ,
,![]() ,
,![]() 的延长线相交于点
的延长线相交于点![]() .
.
(1)若![]() ,
,![]() ,求抛物线
,求抛物线![]() ,
,![]() 的解析式;
的解析式;
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)是否存在这样的实数![]() (
(![]() ),无论
),无论![]() 取何值,直线
取何值,直线![]() 与
与![]() 都不可能互相垂直?若存在,请直接写出
都不可能互相垂直?若存在,请直接写出![]() 的两个不同的值;若不存在,请说明理由.
的两个不同的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,对角线AC,BD相交于点O,点E是AD边上一点,连接CE,把△CDE沿CE翻折,得到△CPE,EP交AC于点F,CP交BD于点G,连接PO,若PO∥BC,则四边形OFPG的面积是 . 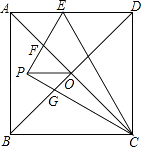
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蒜薹生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并按这三种方式销售,计划平均每吨的售价及成本如下表:
销售方式 | 批发 | 零售 | 储藏后销售 |
售价(元/吨) | 3000 | 4500 | 5500 |
成本(元/吨) | 700 | 1000 | 1200 |
若经过一段时间,蒜薹按计划全部售出获得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量的 ![]() .
.
(1)求y与x之间的函数关系式;
(2)由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的中线,
的中线,![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 重合).
重合).![]() 交
交![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() .
.

(1)如图1,当点![]() 与
与![]() 重合时,求证:四边形
重合时,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,当点![]() 不与
不与![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com