
【题目】如图,![]() 是
是![]() 的中线,
的中线,![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 重合).
重合).![]() 交
交![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() .
.

(1)如图1,当点![]() 与
与![]() 重合时,求证:四边形
重合时,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,当点![]() 不与
不与![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)证明见解析(2)成立,理由见解析;(3)①30°.②1+![]() .
.
【解析】
试题分析:(1)只要证明AE=BM,AE∥BM即可解决问题;
(2)成立.如图2中,过点M作MG∥DE交CE于G.由四边形DMGE是平行四边形,推出ED=GM,且ED∥GM,由(1)可知AB=GM,AB∥GM,可知AB∥DE,AB=DE,即可推出四边形ABDE是平行四边形;
(3)①如图3中,取线段HC的中点I,连接MI,只要证明MI=![]() AM,MI⊥AC,即可解决问题;
AM,MI⊥AC,即可解决问题;
②设DH=x,则AH=![]() x,AD=2x,推出AM=4+2x,BH=4+2x,由四边形ABDE是平行四边形,推出DF∥AB,推出
x,AD=2x,推出AM=4+2x,BH=4+2x,由四边形ABDE是平行四边形,推出DF∥AB,推出![]() ,可得
,可得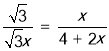 ,解方程即可;
,解方程即可;
试题解析:(1)证明:如图1中,
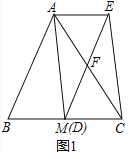
∵DE∥AB,
∴∠EDC=∠ABM,
∵CE∥AM,
∴∠ECD=∠ADB,
∵AM是△ABC的中线,且D与M重合,
∴BD=DC,
∴△ABD≌△EDC,
∴AB=ED,∵AB∥ED,
∴四边形ABDE是平行四边形.
(2)结论:成立.理由如下:
如图2中,过点M作MG∥DE交CE于G.

∵CE∥AM,
∴四边形DMGE是平行四边形,
∴ED=GM,且ED∥GM,
由(1)可知AB=GM,AB∥GM,
∴AB∥DE,AB=DE,
∴四边形ABDE是平行四边形.
(3)①如图3中,取线段HC的中点I,连接MI,
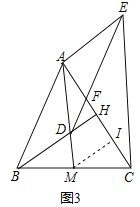
∵BM=MC,
∴MI是△BHC的中位线,
∴∥BH,MI=![]() BH,
BH,
∵BH⊥AC,且BH=AM.
∴MI=![]() AM,MI⊥AC,
AM,MI⊥AC,
∴∠CAM=30°.
②设DH=x,则AH=![]() x,AD=2x,
x,AD=2x,
∴AM=4+2x,
∴BH=4+2x,
∵四边形ABDE是平行四边形,
∴DF∥AB,
∴![]() ,
,
∴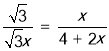 ,
,
解得x=1+![]() 或1-
或1-![]() (舍弃),
(舍弃),
∴DH=1+![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知正方形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() .
.
(1)如图1,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .若
.若![]() ,求证:
,求证:![]() ;
;
(2)如图2,![]() 是
是![]() 上的点,过点
上的点,过点![]() 作
作![]() ,交线段
,交线段![]() 于点
于点![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .若
.若![]() ,
,
①求证:![]() ;
;
②当![]() 时,求
时,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )
A.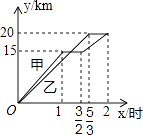
B.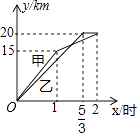
C.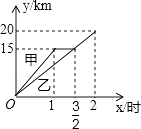
D.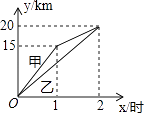
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形![]() )靠墙摆放,高
)靠墙摆放,高![]() ,宽
,宽![]() ,小强身高
,小强身高![]() ,下半身
,下半身![]() ,洗漱时下半身与地面成
,洗漱时下半身与地面成![]() (
(![]() ),身体前倾成
),身体前倾成![]() (
(![]() ),脚与洗漱台距离
),脚与洗漱台距离![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 在同一直线上).
在同一直线上).
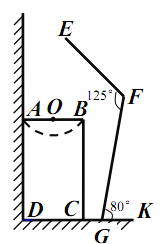
(1)此时小强头部![]() 点与地面
点与地面![]() 相距多少?
相距多少?
(2)小强希望他的头部![]() 恰好在洗漱盆
恰好在洗漱盆![]() 的中点
的中点![]() 的正上方,他应向前或后退多少?
的正上方,他应向前或后退多少?
(![]() ,
,![]() ,
,![]() ,结果精确到
,结果精确到![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x+3与y轴交于点A,直线y=kx﹣1与y轴交于点B,与直线y=2x+3交于点C(﹣1,n).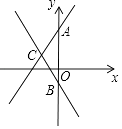
(1)求n、k的值;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com