
【题目】阅读下面的证明过程,在每步后的横线上填写该步推理的依据. 如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线,求证:DF∥AB
证明:∵BE是∠ABC的角平分线
∴∠1=∠2
又∵∠E=∠1
∴∠E=∠2
∴AE∥BC
∴∠A+∠ABC=180°
又∵∠3+∠ABC=180°
∴∠A=∠3
∴DF∥AB . 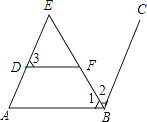
【答案】角的平分线的定义;等量代换;内错角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等;同位角相等,两直线平行
【解析】解:证明:∵BE是∠ABC的角平分线 ∴∠1=∠2(角的平分线的定义),
又∵∠E=∠1
∴∠E=∠2 (等量代换)
∴AE∥BC (内错角相等,两直线平行),
∴∠A+∠ABC=180° (两直线平行,同旁内角互补),
又∵∠3+∠ABC=180°
∴∠A=∠3 (同角的补角相等),
∴DF∥AB(同位角相等,两直线平行).
故答案是:角的平分线的定义;等量代换;内错角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等;同位角相等,两直线平行.
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图: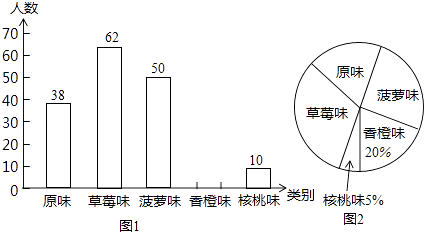
(1)本次被调查的学生有名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】遵义市某学校7位学生的中考体育测试成绩(满分40分)依次为37,40,39,37,40,38,40.则这组数据的众数与中位数分别是( )
A. 40,37B. 40,39C. 39,40D. 40,38
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图梯形ABCD中,AD∥BC,∠ABC+∠C=90°,AB=6,CD=8,M,N,P分别为AD、BC、BD的中点,则MN的长为( ) 
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠1=∠2=50°.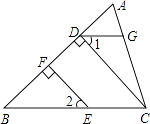
(1)求证:EF∥CD;
(2)若∠AGD=65°,试求∠DCG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=![]() GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
其中,正确的结论有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com