练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图梯形ABCD中，AD∥BC，∠ABC+∠C=90°，AB=6，CD=8，M，N，P分别为AD、BC、BD的中点，则MN的长为（ ）
    A.4
    B.5
    C.6
    D.7

    【答案】B
    【解析】解：∵M，N，P分别为AD、BC、BD的中点， ∴MP∥AB，PN∥CD，MP= AB=3，PN= CD=4．
    ∴∠MPD=∠ABD，∠PNB=∠C．
    又∠ABC+∠C=90°，∠DPN=∠PBN+∠PNB，
    ∴∠MPN=90°．
    ∴MN= =5．
    故选B．
    【考点精析】通过灵活运用三角形中位线定理和梯形的定义，掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；一组对边平行，另一组对边不平行的四边形是梯形．两腰相等的梯形是等腰梯形即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC和△DEC中，已知AB=DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是（ ）
    A.BC=EC，∠B=∠E
    B.BC=EC，AC=DC
    C.BC=DC，∠A=∠D
    D.∠B=∠E，∠A=∠D

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】胜利中学会议室内的会议桌是一个长方形，长1.6米，宽1米，学校准备制作一块桌布，面积是桌面的2倍，且使桌面四周垂下的边等宽。若设四周垂下的边为x米，则应列得的方程为_____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥CD，直线EF与AB，CD分别交于点 M，N，过点N的直线GH 与AB交于点P，则下列结论中一定正确的个数是（ ）
    ①∠EMB=∠MND；②∠BMN=∠MNC；③∠CNH=∠BPG；④∠DNG=∠AME．

    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知点D、点E分别是等边三角形ABC中BC、AB边的中点，AD=5，点F是AD边上的动点，则BF+EF的最小值为（ ）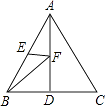
    A.7.5
    B.5
    C.4
    D.不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各因式分解正确的是（ ）
    A.﹣x2+（﹣2）2=（x﹣2）（x+2）
    B.x2+2x﹣1=（x﹣1）2
    C.4x2﹣4x+1=（2x﹣1）2
    D.x2﹣4x=x（x+2）（x﹣2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面的证明过程，在每步后的横线上填写该步推理的依据． 如图，∠E=∠1，∠3+∠ABC=180°，BE是∠ABC的角平分线，求证：DF∥AB
    证明：∵BE是∠ABC的角平分线
    ∴∠1=∠2
    又∵∠E=∠1
    ∴∠E=∠2
    ∴AE∥BC
    ∴∠A+∠ABC=180°
    又∵∠3+∠ABC=180°
    ∴∠A=∠3
    ∴DF∥AB ．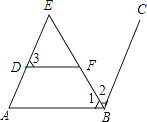

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了了解我市2017年中考数学学科各分数段成绩分布情况，从中抽取180名考生的中考数学成绩进行统计分析．在这个问题中，样本是指（ ）

    A. 180 B. 被抽取的180名考生

    C. 被抽取的180名考生的中考数学成绩 D. 我市2017年中考数学成绩

    查看答案和解析>>

    科目：初中数学 来源： 题型：

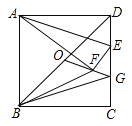
    【题目】如图，在正方形ABCD中，AB=6，点E在边CD上，DE=DC，连接AE，将△ADE沿AE翻折，点D落在点F处，点O是对角线BD的中点，连接OF并延长OF交CD于点G，连接BF，BG，则△BFG的周长是 ．

    查看答案和解析>>

    同步练习册答案