
����Ŀ��ij��Ϊ����ǿѧ�����ʣ�ȫ��ʵʩ��ѧ�������̡�Ӫ�����̣�ijƷ��ţ�̹�Ӧ���ṩ��ԭζ����ݮζ������ζ�����ζ������ζ���ֿ�ζ��ţ���ṩѧ�����ã������ѧΪ���˽�ѧ���Բ�ͬ��ζţ�̵�ϲ�ã���ȫУ����ţ�̵�ѧ��������������飨ÿ�и��ֿ�ζţ�̵������ͬ������������ͼ���Ų�����������ͳ��ͼ��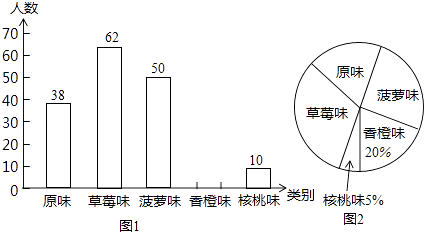
��1�����α������ѧ��������
��2����ȫ���������ͳ��ͼ1���������ϲ�á�����ζ��ţ�̵�ѧ������������ͳ��ͼ����ռԲ�ĽǵĶ�����
��3����У����1200��ѧ�������˸�Ʒ�Ƶ�ţ�̣�ţ�̹�Ӧ��ÿ��ֻΪÿ������ţ�̵�ѧ������һ��ţ�̣�Ҫʹѧ��ÿ�춼�ȵ��Լ�ϲ�õĿ�ζ��ţ�̣�ţ�̹�Ӧ��ÿ��������У��ţ���У���ݮζҪ��ԭζ���Ͷ��ٺУ�
���𰸡�
��1���⣺10��5%=200�������𣺱��α������ѧ����200��,�ʴ�Ϊ��200��
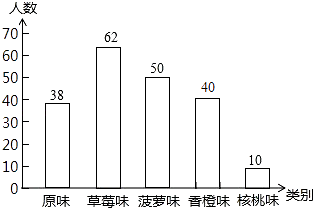
��2���⣺200��38��62��50��10=40��������
����ͳ��ͼ���£�
![]() =90�㣬
=90�㣬
��ϲ�á�����ζ��ţ�̵�ѧ������������ͳ��ͼ2����ռԲ�ĽǵĶ���Ϊ90��
��3���⣺1200���� ![]() ��=144���У���
��=144������
�𣺲�ݮζҪ��ԭζ����144��
����������1��ϲ�á�����ζ��ţ�̵�ѧ��������������ռ�İٷֱȼ��ɵñ��α������ѧ��������
��2���ñ��α������ѧ������������ȥϲ��ԭζ����ݮζ������ζ������ζ�������ó�ϲ�����ζ����������ȫ����ͳ��ͼ���ɣ���ϲ�á�����ζ��ţ�̵�ѧ�����������������ٳ���360�㣬���ɵ�ϲ�á�����ζ��ţ�̵�ѧ������������ͳ��ͼ2����ռԲ�ĽǵĶ�����
��3����ϲ�ò�ݮζ������ռ�İٷֱȼ�ȥϲ��ԭζ������ռ�İٷֱȣ��ٳ��Ը�У�����������ɣ�


 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ����(����)
A. �����ȵ�����ͼ����ȫ��ͼ�� B. ȫ�������ε��ܳ����
C. ���������ζ���ȫ��ͼ�� D. ȫ�������εı����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�͡�DEC�У���֪AB=DE����������������������ʹ��ABC�ա�DEC���������ӵ�һ�������ǣ� �� 
A.BC=EC����B=��E
B.BC=EC��AC=DC
C.BC=DC����A=��D
D.��B=��E����A=��D
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ʒר��������7�������9�������������Ϊ355Ԫ������10�������20�������������Ϊ650Ԫ��
��1����ÿ�������ÿ���������������
��2����֪ÿ������Ľ���Ϊ200Ԫ��ÿ������Ľ���Ϊ160Ԫ������ר����ƻ��ò�����17400Ԫ�������������100������Ҫ��������������������������һ�룬����Ϊר������Ʒ���Ҫ��Ľ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
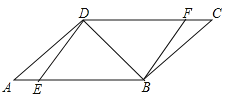
����Ŀ����ͼ����ABCD�У���E��F�ֱ���AB��DC�ϣ���ED��DB��FB��BD��
��1����֤����AED�ա�CFB��
��2������A=30�㣬��DEB=45�㣬��֤��DA=DF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��1��1����B����1��1����C����1����2����D��1����2������һ����Ϊ2017����λ������û�е��Ե�ϸ�ߣ��ߵĴ�ϸ���Բ��ƣ���һ�˹̶���A��������A��B��C��D��A�����Ĺ��ɽ������ı���ABCD�ı��ϣ���ϸ�ߵ���һ������λ�õĵ�������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʤ����ѧ�������ڵĻ�������һ�������Σ���1.6�ף���1�ף�ѧУ������һ������������������2������ʹ�������ܴ��µıߵȿ����������ܴ��µı�Ϊx�ף���Ӧ�еõķ���Ϊ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������֤�����̣���ÿ����ĺ�������д�ò����������ݣ� ��ͼ����E=��1����3+��ABC=180�㣬BE�ǡ�ABC�Ľ�ƽ���ߣ���֤��DF��AB
֤������BE�ǡ�ABC�Ľ�ƽ����
���1=��2
�֡ߡ�E=��1
���E=��2
��AE��BC
���A+��ABC=180��
�֡ߡ�3+��ABC=180��
���A=��3
��DF��AB �� 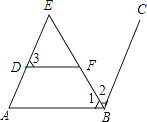
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com