
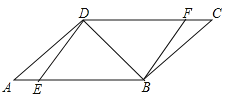
【题目】如图,在ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.
【答案】(1)证明见试题解析;(2)证明见试题解析.
【解析】
试题分析:(1)由平行四边形的性质得到对边平行且相等,对角相等,再由垂直的定义得到一对直角相等,利用等式的性质得到一对角相等,利用ASA即可得证;
(2)过D作DH垂直于AB,在直角三角形ADH中,有AD=2DH,在直角三角形DEB中,有EB=2DH,易得四边形EBFD为平行四边形,利用平行四边形的对边相等得到EB=DF,等量代换即可得证.
试题解析:(1)∵平行四边形ABCD,∴AD=CB,∠A=∠C,AD∥CB,∴∠ADB=∠CBD,∵ED⊥DB,FB⊥BD,∴∠EDB=∠FBD=90°,∴∠ADE=∠CBF,在△AED和△CFB中,∵∠ADE=∠CBD,AD=BC,∠A=∠C,∴△AED≌△CFB(ASA);
(2)作DH⊥AB,垂足为H,在Rt△ADH中,∠A=30°,∴AD=2DH,在Rt△DEB中,∠DEB=45°,∴EB=2DH,∴四边形EBFD为平行四边形,∴FD=EB,∴DA=DF.


科目:初中数学 来源: 题型:
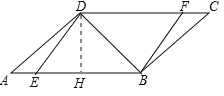
【题目】如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
(1)求证:PQ∥AB;
(2)若点D在∠BAC的平分线上,求CP的长;
(3)若△PDE与△ABC重叠部分图形的周长为T,且12≤T≤16,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
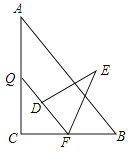
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
(1)求证:四边形ABCD是平行四边形;
(2)若点E是AC的中点,判断BE与AC的位置关系,并说明理由;
(3)若△ABE是等边三角形,AD=![]() ,求对角线AC的长.
,求对角线AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图: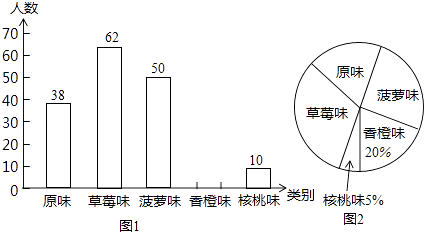
(1)本次被调查的学生有名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
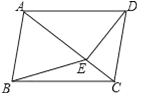
【题目】如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E,CE=1,延长CE、BA交于点F. 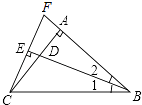
(1)求证:△ADB≌△AFC;
(2)求BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,收费标准如下:
人数m | 0<m≤100 | 100<m≤200 | m>200 |
收费标准(元/人) | 90 | 85 | 75 |
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费20 800元,若两校联合组团只需花费18 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗?为什么?
(2)两所学校报名参加旅游的学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠1=∠2=50°.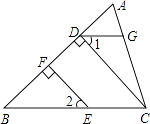
(1)求证:EF∥CD;
(2)若∠AGD=65°,试求∠DCG的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com