
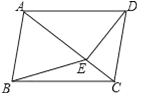
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
(1)求证:四边形ABCD是平行四边形;
(2)若点E是AC的中点,判断BE与AC的位置关系,并说明理由;
(3)若△ABE是等边三角形,AD=![]() ,求对角线AC的长.
,求对角线AC的长.
【答案】(1)证明见解析;(2)BE⊥AC;(3)![]() .
.
【解析】
试题分析:(1)根据平行四边形的性质得出∠ABC+∠DCB=180°,推出∠ADC+∠BCD=180°,根据平行线的判定得出AD∥BC,根据平行四边形的判定推出即可;
(2)求出AD=DC,根据菱形的判定得出四边形ABCD是菱形,根据等腰三角形的性质得出即可;
(3)根据等边三角形的性质得出AB=AE,∠BAC=60°,求出∠DCE=∠BAE=60°,求出CD=2EC,设CE=x,则AB=DC=AE=2x,根据勾股定理得出方程,求出x,即可得出答案.
试题解析:(1)证明:∵AB∥CD,∴∠ABC+∠DCB=180°,∵∠ABC=∠ADC,∴∠ADC+∠BCD=180°,∴AD∥BC,∵AB∥CD,∴四边形ABCD是平行四边形;
(2)解:BE⊥AC,理由是:∵DE⊥AC,E为AC的中点,∴AD=DC,∵四边形ABCD是平行四边形,∴四边形ABCD是菱形,∴AB=BC,∵E为AC的中点,∴BE⊥AC;
(3)解:∵△ABE是等边三角形,∴AB=AE,∠BAC=60°,∵AB∥DC,∴∠DCE=∠BAE=60°,∵∠DEC=90°,∴∠CDE=30°,∴CD=2EC,设CE=x,则AB=DC=AE=2x,由勾股定理得:DE2=AD2﹣AE2=DC2﹣CE2,即![]() ,解得:x=
,解得:x=![]() (负数舍去),即CE=
(负数舍去),即CE=![]() ,AE=
,AE=![]() ,∴AC=
,∴AC=![]() .
.


科目:初中数学 来源: 题型:
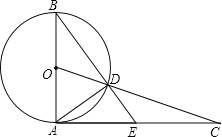
【题目】如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD.
(1)求证:△CDE∽△CAD;
(2)若AB=2,AC=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题:探索发现规律拓展应用题
(1)如图①,∠CEF=90°,点B在射线EF上,AB∥CD,若∠ABE=130°,求∠C的度数;
(2)如图②,把“∠CEF=90°”改为“∠CEF=120°”,点B在射线EF上,AB∥CD.猜想∠ABE与∠C的数量关系,并说明理由.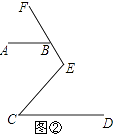
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( ) 
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
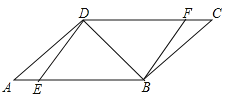
【题目】如图,在ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列不等式的变形正确的是( )
A.若am>bm,则a>b
B.若am2>bm2 , 则a>b
C.若a>b,则am2>bm2
D.若a>b且ab>0,则 ![]() >
> ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各因式分解正确的是( )
A.﹣x2+(﹣2)2=(x﹣2)(x+2)
B.x2+2x﹣1=(x﹣1)2
C.4x2﹣4x+1=(2x﹣1)2
D.x2﹣4x=x(x+2)(x﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com