练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在△ABC中，∠C=90°若BC＝2，则AB＝4，则∠B＝____________°

    【答案】60°

    【解析】分析：根据直角三角形的三边关系得出角的度数．

    详解：∵AB=2BC， ∴∠A=30°， ∴∠B=90°－30°=60°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某体育用品专卖店销售7个篮球和9个排球的总利润为355元，销售10个篮球和20个排球的总利润为650元．
    （1）求每个篮球和每个排球的销售利润；
    （2）已知每个篮球的进价为200元，每个排球的进价为160元，若该专卖店计划用不超过17400元购进篮球和排球共100个，且要求篮球数量不少于排球数量的一半，请你为专卖店设计符合要求的进货方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，∠A=30°，D是AC边上的点；先将△ABC沿着BD翻折，翻折后△ABD的边AB交AC于点E；又将△BCE沿着BE翻折，C点恰好落在BD上，此时∠BEC=78°，则原三角形的∠ABC=度．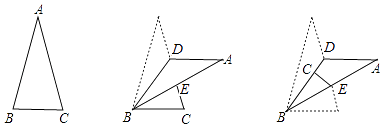

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知点D、点E分别是等边三角形ABC中BC、AB边的中点，AD=5，点F是AD边上的动点，则BF+EF的最小值为（ ）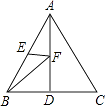
    A.7.5
    B.5
    C.4
    D.不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行，在B处观测灯塔A位于南偏东50°方向上，轮船航行40分钟到达C处，在C处观测灯塔A位于北偏东10°方向上，则C处与灯塔A的距离是（ ）

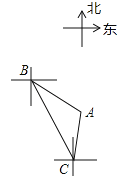
    A．20海里 B．40海里 C．海里 D．海里

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面的证明过程，在每步后的横线上填写该步推理的依据． 如图，∠E=∠1，∠3+∠ABC=180°，BE是∠ABC的角平分线，求证：DF∥AB
    证明：∵BE是∠ABC的角平分线
    ∴∠1=∠2
    又∵∠E=∠1
    ∴∠E=∠2
    ∴AE∥BC
    ∴∠A+∠ABC=180°
    又∵∠3+∠ABC=180°
    ∴∠A=∠3
    ∴DF∥AB ．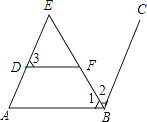

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图AB∥CD，EF分别交AB于点F，交CD于点E，EF与DB交于点G，且EA平分∠CEF，∠BFG=70°．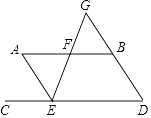

    （1）求∠A的度数．
    （2）若∠A=∠D，求证：∠AEF=∠G．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果关于x的方程x2+mx+25＝0有两个相等的实数根，那么m的值为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“综合与实践”学习活动准备制作一组三角形，记这些三角形的三边分别为a，b，c，并且这些三角形三边的长度为大于1且小于5的整数个单位长度．
    （1）用记号（a，b，c）（a≤b≤c）表示一个满足条件的三角形，如（2，3，3）表示边长分别为2，3，3个单位长度的一个三角形．请列举出所有满足条件的三角形．
    （2）用直尺和圆规作出三边满足a＜b＜c的三角形（用给定的单位长度，不写作法，保留作图痕迹）．

    查看答案和解析>>

    同步练习册答案