
【题目】如图AB∥CD,EF分别交AB于点F,交CD于点E,EF与DB交于点G,且EA平分∠CEF,∠BFG=70°.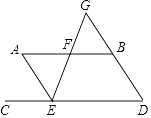
(1)求∠A的度数.
(2)若∠A=∠D,求证:∠AEF=∠G.
【答案】
(1)解:∵∠AFE=∠BFG=70°,
∵AB∥CD,
∴∠CEF=180°﹣∠AFE=110°,
∵且EA平分∠CEF,
∴∠AEF= ![]() CEF=55°,
CEF=55°,
∴∠A=180°﹣∠AFE﹣∠AEF=55°
(2)解:∵AB∥CD,
∴∠GED=∠GFB=70°,
∵∠D=∠A=55°,
∴∠G=55°,
∴∠AEF=∠G
【解析】(1)由AB∥CD可得同旁内角互补,即∠CEF=180°﹣∠AFE=110°,由EA平分∠CEF,∠A可转化为∠ AEC,即可求出;(2)由(1)∠AEF=∠A,可求出∠G=55°,即∠AEF=∠G.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
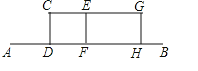
查看答案和解析>>
科目:初中数学 来源: 题型:
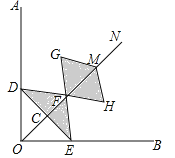
【题目】如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)证明:“三角形内角和是180°”;
(2)请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题,判断这一逆命题是真命题还是假命题,如果是真命题给出证明,如果是假命题,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,且AC⊥BD,点E,F,G,H分别是AB,BC,CD,DA的中点,依次连接各边中点得到四边形EFGH,求证:四边形EFGH是矩形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°,连接AE,再以AE为边作第三个菱形AEGH,使∠HAE=60°,按此规律下去,则第n个菱形的边长为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com