
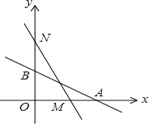
【题目】如图,直线L:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
(1)点A的坐标:_____;点B的坐标:_____;
(2)求△NOM的面积S与M的移动时间t之间的函数关系式;
(3)在y轴右边,当t为何值时,△NOM≌△AOB,求出此时点M的坐标;
(4)在(3)的条件下,若点G是线段ON上一点,连结MG,△MGN沿MG折叠,点N恰好落在x轴上的点H处,求点G的坐标.
【答案】(1)(4,0),(0,2);(2)![]() ;(3)M(2,0);(4)G(0,
;(3)M(2,0);(4)G(0, ![]() ).
).
【解析】试题分析:(1)在![]() 中,令别令y=0和x=0,则可求得A、B的坐标;
中,令别令y=0和x=0,则可求得A、B的坐标;
(2)利用t可表示出OM,则可表示出S,注意分M在y轴右侧和左侧两种情况;
(3)由全等三角形的性质可得OM=OB=2,则可求得M点的坐标;
(4)由折叠的性质可知MG平分∠OMN,利用角平分线的性质定理可得到![]() ,则可求得OG的长,可求得G点坐标.
,则可求得OG的长,可求得G点坐标.
试题解析:解:(1)在![]() 中,令y=0,得x=4,令x=0可,y=2,∴A(4,0),B(0,2);
中,令y=0,得x=4,令x=0可,y=2,∴A(4,0),B(0,2);
(2)由题题意可知AM=t.
①当点M在y轴右边,即0<t≤4时,OM=OA﹣AM=4﹣t.
∵N(0,4),∴ON=4,∴S=![]() OMON=
OMON=![]() ×4×(4﹣t)=8﹣2t;
×4×(4﹣t)=8﹣2t;
②当点M在y轴左边,即t>4时,则OM=AM﹣OA=t﹣4,
∴S=![]() ×4×(t﹣4)=2t﹣8;
×4×(t﹣4)=2t﹣8;
综上所述: ![]() ;
;
(3)∵△NOM≌△AOB,∴MO=OB=2,∴M(2,0);
(4)∵OM=2,ON=4,∴MN=![]() =
=![]() .
.
∵△MGN沿MG折叠,∴∠NMG=∠OMG,∴ ![]() ,且NG=ON﹣OG,
,且NG=ON﹣OG,
∴![]() ,解得OG=
,解得OG=![]() ,∴G(0,
,∴G(0, ![]() ).
).


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:
①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=![]() MF.其中正确结论的是( )
MF.其中正确结论的是( )

A. ①③④ B. ②④⑤ C. ①③④⑤ D. ①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
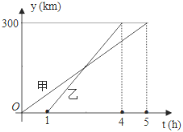
【题目】甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶时间x(小时)之间的函数关系如图所示,根据图象提供的信息,解决下列问题:
(1)A,B两城相距 千米;
(2)分别求甲、乙两车离开A城的距离y与x的关系式.
(3)求乙车出发后几小时追上甲车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() 、
、![]() .
.![]() 是线段
是线段![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .过点
.过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/18/2206393160556544/2207286529548288/STEM/a9696d0cbdac438aa94c80bfc838afd4.png]
(1)求该抛物线的解析式;
(2)试求线段![]() 的长
的长![]() 关于点
关于点![]() 的横坐标
的横坐标![]() 的函数解析式,并求出
的函数解析式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
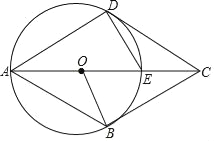
【题目】已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D,点B在⊙O上,连接OB.
(1)求证:DE=OE;
(2)若CD∥AB,求证:BC是⊙O的切线;
(3)在(2)的条件下,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表三行数的规律,回答下列问题:
第 | 第 | 第 | 第 | 第 | 第 | ... | |
第 |
|
|
|
|
|
| ... |
第 |
|
|
|
|
|
| ... |
第 |
|
|
|
|
|
| ... |
(1)第![]() 行的第四列数
行的第四列数![]() ______________,第
______________,第![]() 行的第六列数
行的第六列数![]() ______________;
______________;
(2)若第![]() 行的某一列的数为
行的某一列的数为![]() ,则第
,则第![]() 的式子表示);
的式子表示);
(3)已知第![]() 列的三个数的和为
列的三个数的和为![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在边AB上,且AD=3,DB=2,过点D作DE∥BC,交边AC于点E,将△ADE沿着DE折叠,得△MDE,与边BC分别交于点F,G.若△ABC的面积为15,则△MFG的面积是( )
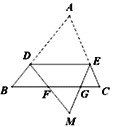
A. 0.5B. 0.6C. 0.8D. 1.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com