
【题目】如图,已知直线y=kx+2![]() 与x轴、y轴分别相交于点A、点B,∠BAO=30°,若将△AOB沿直钱CD折叠,使点A与点B重合,折痕CD与x轴交于点C,与AB交于点D.
与x轴、y轴分别相交于点A、点B,∠BAO=30°,若将△AOB沿直钱CD折叠,使点A与点B重合,折痕CD与x轴交于点C,与AB交于点D.

(1)求k的值;
(2)求点C的坐标;
(3)求直线CD的表达式.
【答案】(1) k=﹣![]() ;(2) 点C(2,0);(3) 直线CD的表达式为:y=
;(2) 点C(2,0);(3) 直线CD的表达式为:y=![]() x﹣2
x﹣2![]() .
.
【解析】
(1)令x=0,则y=2![]() ,即:OB=2
,即:OB=2![]() ,再根据直角三角形中,30°锐角所对的直角边等于斜边的一半解得AB=2OB=4
,再根据直角三角形中,30°锐角所对的直角边等于斜边的一半解得AB=2OB=4![]() ,再根据勾股定理解得:OA=6,从而求得点A坐标,代入解析式即可求解;
,再根据勾股定理解得:OA=6,从而求得点A坐标,代入解析式即可求解;
(2)设:BC=AC=a,则OC=6﹣a,在△BOC中,(2![]() )2+(6﹣a)2=a2,解得:a=4,即可求解;
)2+(6﹣a)2=a2,解得:a=4,即可求解;
(3)点D时AB的中点,则点D(3,![]() ),将点C、D的坐标代入一次函数表达式,即可求解.
),将点C、D的坐标代入一次函数表达式,即可求解.
解:(1)令x=0,则y=2![]() ,即:OB=2
,即:OB=2![]() ,因为∠BAO=30°,所以AB=2OB=4
,因为∠BAO=30°,所以AB=2OB=4![]() ,
,
在Rt△BAO中,由勾股定理得:OA=6,把A(6,0)代入解析式y=kx+2![]() 得:k=﹣
得:k=﹣![]() ;
;
(2)设:BC=AC=a,则OC=6﹣a,
在△BOC中,(2![]() )2+(6﹣a)2=a2,解得:a=4,
)2+(6﹣a)2=a2,解得:a=4,
则点C(2,0);
(3)点D时AB的中点,则点D(3,![]() ),
),
将点C、D的坐标代入一次函数:y=kx+b得: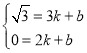 ,解得:
,解得: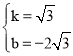 ,
,
故直线CD的表达式为:y=![]() x﹣2
x﹣2![]() .
.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】(题文)停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
(1)若点D在线段BC上,如图1.
①依题意补全图1;
②判断BC与CG的数量关系与位置关系,并加以证明;
(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB=![]() ,则GE的长为_____,并简述求GE长的思路.
,则GE的长为_____,并简述求GE长的思路.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人玩“锤子、石头、剪子、布”游戏,他们在不透明的袋子中放入形状、大小均相同的15张卡片,其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为2,3,4,6.两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式了的平方,如3+2![]() =(1+
=(1+![]() )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:
若设a+b![]() =(m+n
=(m+n![]() )2=m2+2n2+2mn
)2=m2+2n2+2mn![]() (其中a、b、m、n均为整数),
(其中a、b、m、n均为整数),
则有a=m2+2n2,b=2mn.
这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)若a+b![]() =(m+n
=(m+n![]() )2,当a、b、m、n均为整数时,用含m、n的式子分别表示a、b,得:a= ,b= ;
)2,当a、b、m、n均为整数时,用含m、n的式子分别表示a、b,得:a= ,b= ;
(2)若a+6![]() =(m+n
=(m+n![]() )2,且a、m、n均为正整数,求a的值;
)2,且a、m、n均为正整数,求a的值;
(3)化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,DE=3BE,点P,Q分别在BD,AD 上,则AP+PQ的最小值为:
A. 2![]() B.
B. ![]() C. 2
C. 2![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
(1)将△ABC向下平移5个单位长度,画出平移后的A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)将△ABC绕点C逆时针旋转90°,画出旋转后的△A3B3C.

查看答案和解析>>
科目:初中数学 来源: 题型:
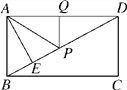
【题目】如图,已知RT△ABC中,∠C=90°,AC=4,BC=8.动点P从点C出发,以每秒2个单位的速度沿射线CB方向运动,连接AP,设运动时间为ts.
(1)求斜边AB的长
(2)当t为何值时,△PAB的面积为6
(3)若t<4,请在所给的图中画出△PAB中AP边上的高BQ,问:当t为何值时,BQ长为4?并求出此时点Q到边BC的距离
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com