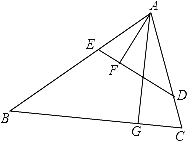
【题目】如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC．
（1）求证：△ADE∽△ABC；
（2）若AD=3，AB=5，求
的值．
期末冲刺100分创新金卷完全试卷系列答案科目：初中数学 来源： 题型：
【题目】抛物线y＝ax2＋bx＋c的图角如图3，则下列结论：①abc＞0；②a＋b＋c＝2；③a＞
；④b＜1．其中正确的结论是( )
A. ①② B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在数学兴趣小组活动中，小明进行数学探究活动．将大小不相同的正方形ABCD与正方形AEFG按图1位置放置，AD与AE在同一条直线上，AB与AG在同一条直线上．
（1）小明发现DG＝BE且DG⊥BE，请你给出证明；
（2）如图2，小明将正方形ABCD绕点A转动，当点B恰好落在线段DG上时
①猜想线段DG和BE的位置关系是 ．
②若AD＝2
，AE＝
，求△ADG的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知双曲线y=
（k＜0）经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（﹣6，4），则△AOC的面积为（ ）
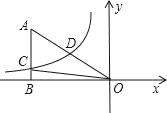
A. 12 B. 9 C. 6 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】《庄子·天下》：“一尺之棰，日取其半，万世不竭.”意思是说：一尺长的木棍，每天截掉一半，永远也截不完.我国智慧的古代人在两千多年前就有了数学极限思想，今天我们运用此数学思想研究下列问题.
（规律探索）
(1)如图1所示的是边长为1的正方形，将它剪掉一半，则S阴影1＝1－
＝__________；
如图2，在图1的基础上，将阴影部分再裁剪掉—半，则S阴影2＝1－－()2＝_______；
同种操作，如图3，S阴影3＝1－－()2－()3＝__________；
如图4，S阴影4＝1－－()2－()3－()4＝___________；
……
若同种地操作n次，则S阴影n＝1－－()2－()3－…－()n＝_________.
（规律归纳）
(2)直接写出＋
＋
＋…＋
的化简结果：_________.
（规律应用）
(3)直接写出算式＋＋＋…＋的值：__________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将连续的奇数1，3，5，7，9……，排成如图的数表：
（1）十字框的5个数的和与中间的数23有什么关系，若将十字框上下左右平移，可框住另外5个数，这5个数还有这种规律吗.
（2）设十字框中中间的数为
，用含的式子表示十字框中的5个数之和.
（3）十字框中的5个数的和能等于1045吗.若能，请写出这5个数，若不能，说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，建筑物AB的高为6m，在其正东方向有一个通信塔CD，在它们之间的地面点M（B，M，D三点在一条直线上）处测得建筑物顶端A，塔顶C的仰角分别为37°和60°，在A处测得塔顶C的仰角为30°，则通信塔CD的高度．（精确到0.01m）
查看答案和解析>>
科目：初中数学 来源： 题型：
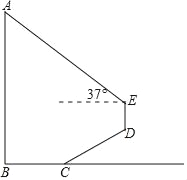
【题目】如图，为测量学校旗杆AB的高度，小明从旗杆正前方3米处的点C出发，沿坡度为i=1：
的斜坡CD前进2米到达点D，在点D处放置测角仪，测得旗杆顶部A的仰角为37°，量得测角仪DE的高为1.5米．A、B、C、D、E在同一平面内，且旗杆和测角仪都与地面垂直．
（1）求点D的铅垂高度（结果保留根号）；
（2）求旗杆AB的高度（精确到0.1）．
（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，≈1.73．）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
