
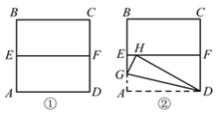
【题目】将一张边长为2的正方形纸片ABCD对折,设折痕为EF(如图①);再沿过点D的折痕将∠A翻折,使得点A落在EF上的点H处(如图②),折痕交AE于点G,则EG的长度是___________.
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】为了改善市民的生活环境,我是在某河滨空地处修建一个如图所示的休闲文化广场.在Rt△ABC内修建矩形水池DEFG,使顶点D、E在斜边AB上,F、G分别在直角边BC、AC上;又分别以AB、BC、AC为直径作半圆,它们交出两弯新月(图中阴影部分),两弯新月部分栽植花草;其余空地铺设地砖.其中![]() 米,∠BAC=600.设EF=x米,DE=y米.
米,∠BAC=600.设EF=x米,DE=y米.
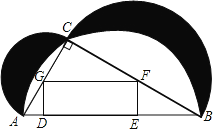
(1)求y与x之间的函数解析式;
(2)当x为何值时,矩形DEFG的面积最大?最大面积是多少?
(3)求两弯新月(图中阴影部分)的面积,并求当x为何值时,矩形DEFG的面积等于两弯新月面积的![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=ax2+c与x轴交于点A(m,0),B(n,0),与y轴交于点C(0,c),则称△ABC为“抛物三角形”.特别地,当mnc<0时,称△ABC为“正抛物三角形”;当mnc>0时,称△ABC为“倒抛物三角形”.若△ABC为“倒抛物三角形”时,a、c应分别满足条件_____、_____;若△ABC为“正抛物三角形”,此时△ABC及其关于x轴的轴对称图形恰好构成了一个含60°角的菱形,则a、c应满足的关系为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 分别是线段
分别是线段![]() ,
,![]() 上的点,连接
上的点,连接![]() ,使四边形
,使四边形![]() 为正方形,若点
为正方形,若点![]() 是
是![]() 上的动点,连接
上的动点,连接![]() ,将矩形沿
,将矩形沿![]() 折叠使得点
折叠使得点![]() 落在正方形
落在正方形![]() 的对角线所在的直线上,对应点为
的对角线所在的直线上,对应点为![]() ,则线段
,则线段![]() 的长为________.
的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两单位为爱心基金捐款,其中甲单位捐款4800元,乙单位捐款6000元,已知乙单位捐款人数比甲单位多30人,且两单位人均捐款数相等,问这两单位一共有多少人?人均捐款额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC、BD相交于点O,∠A=∠D,要使得△AOB≌△DOC,还需补充一个条件,下面补充的条件不一定正确的是( )
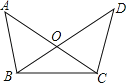
A.OA=ODB.AB=DCC.OB=OCD.∠ABO=∠DCO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 DE∥BC,CD 与 BE 相交于点 O,并且 S△DOE:S△COB=4:9,
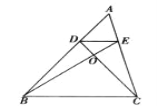
(1)求 AE:AC 的值;
(2)求△ADE 与四边形 DBCE 的面积比。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:
(1)问题发现:如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() 、
、![]() 、
、![]() 在同一直线上,连接
在同一直线上,连接![]() .填空:①
.填空:①![]() 的度数为______(直接写出结论,不用证明).
的度数为______(直接写出结论,不用证明).
②线段![]() 、
、![]() 之间的数量关系是______(直接写出结论,不用证明).
之间的数量关系是______(直接写出结论,不用证明).
(2)拓展探究:如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,![]() 为
为![]() 中
中![]() 边上的高,连接
边上的高,连接![]() .请判断
.请判断![]() 的度数及线段
的度数及线段![]() 、
、![]() 、
、![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)解决问题:在(2)问的条件下,若![]() ,
,![]() ,试求
,试求![]() 的面积(用
的面积(用![]() ,
,![]() 表示).
表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com