
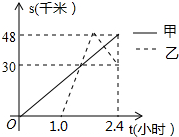
 甲、乙两车分别从A地将一批物品运往B地,再返回A地,如图表示两车离A地的距离s(千米)随时间t(小时)变化的图象,已知乙车到达B地后以30千米/小时的速度返回,则下列说法正确的有( )
甲、乙两车分别从A地将一批物品运往B地,再返回A地,如图表示两车离A地的距离s(千米)随时间t(小时)变化的图象,已知乙车到达B地后以30千米/小时的速度返回,则下列说法正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 找出甲、乙两车在各时间段里离A地的距离s(千米)关于时间t(小时)的解析式,由此可判断①②③,令乙车从B地返回的解析式y=0,可得出乙车返回A地的时间,结合甲车到达B地的时间,可得出④结论成立,本题得以解决.
解答 解:∵乙车到B地后返回到距A地30km所有的时间为$\frac{48-30}{30}$=0.6(小时),
∴乙车到达B地的时间t为2.4-0.6=1.8(小时).
设甲车离A地的距离s(千米)关于时间t(小时)的解析式为y=k1x+b1,
结合图形可知:$\left\{\begin{array}{l}{0={b}_{1}}\\{48=2.4{k}_{1}+{b}_{1}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=20}\\{{b}_{1}=0}\end{array}\right.$,
即甲车离A地的距离s关于时间t的解析式为y=20x.
设乙车离A地的距离s(千米)关于时间t(小时)的解析式为y=k2x+b2,
当1.0≤t≤1.8时,有$\left\{\begin{array}{l}{0={k}_{2}+{b}_{2}}\\{48=1.8{k}_{2}+{b}_{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=60}\\{{b}_{2}=-60}\end{array}\right.$,
即此时乙车离A地的距离s关于时间t的解析式为y=60x-60;
当1.8<t≤2.4时,有$\left\{\begin{array}{l}{48=1.8{k}_{2}+{b}_{2}}\\{30=2.4{k}_{2}+{b}_{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=-30}\\{{b}_{2}=102}\end{array}\right.$,
即此时乙车离A地的距离s关于时间t的解析式为y=-30x+102.
当1.0≤t≤1.8时,解$\left\{\begin{array}{l}{y=20x}\\{y=60x-60}\end{array}\right.$,得x=1.5.
故①成立;
60÷20=3,即从A地到B地的途中乙车速度是甲车的3倍,
故②不成立;
当1.8<t≤2.4时,有$\left\{\begin{array}{l}{y=20x}\\{y=-30x+102}\end{array}\right.$,得$\left\{\begin{array}{l}{x=2.04}\\{y=40.8}\end{array}\right.$,
48-40.8=7.2(千米).
故甲车与乙车在距离B地7.2千米处迎面相遇.
即③不成立;
令y=-30x+102=0,解得:x=3.4.
设甲车返回的速度为m,则有(3.4-2.4)m≥48,
解得:m≥48.
故④成立.
综上可知①④成立.
故选B.
点评 本题考查了一次函数里面的相遇问题,解题的关键是结合图象得出甲、乙两车离A地的距离s(千米)关于时间t(小时)的解析式.本题属于中档题型,借助解析式①②③很好判定,考虑从B地返回A地,列出不等式才可判断④.解决该类题型的关键是数形结合.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 20岁,19岁 | B. | 19岁,19岁 | C. | 19岁,20.5岁 | D. | 19岁,20岁 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
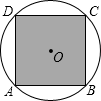 如图,正方形ABCD内接于⊙O,⊙O的直径为$\sqrt{2}$分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
如图,正方形ABCD内接于⊙O,⊙O的直径为$\sqrt{2}$分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )| A. | $\frac{2}{π}$ | B. | $\frac{π}{2}$ | C. | $\frac{1}{2π}$ | D. | $\sqrt{2}π$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
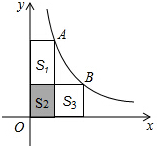 如图,A、B两点在反比例函数y=$\frac{4}{x}$的图象上,分别过A、B两点向坐标轴作垂线段,已知S2的面积为1,则S1+S3的面积为( )
如图,A、B两点在反比例函数y=$\frac{4}{x}$的图象上,分别过A、B两点向坐标轴作垂线段,已知S2的面积为1,则S1+S3的面积为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-3) | B. | (2,-3) | C. | (2,3) | D. | (-1,-6) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com