
【题目】图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)图2中,当∠D=50度,∠B=40度时,求∠P的度数.
(3)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.

【答案】(1)∠A+∠D=∠C+∠B;(2)∠P=45°;(3)2∠P=∠D+∠B.
【解析】
(1)根据三角形内角和定理即可得出∠A+∠D=∠C+∠B;
(2)由(1)得,∠DAP+∠D=∠P+∠DCP①,∠PCB+∠B=∠PAB+∠P②,再根据角平分线的定义可得∠DAP=∠PAB,∠DCP=∠PCB,将①+②整理可得2∠P=∠D+∠B,进而求得∠P的度数;
(3)同(2)根据“8字形”中的角的规律和角平分线的定义,即可得出2∠P=∠D+∠B.
解(1)∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,
∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B;
(2)由(1)得,∠DAP+∠D=∠P+∠DCP,①
∠PCB+∠B=∠PAB+∠P,②
∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
①+②得:∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,
即2∠P=∠D+∠B=50°+40°,
∴∠P=45°;
(3)关系:2∠P=∠D+∠B;证明过程同(2).


科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,将线段AB绕点A按逆时针方向旋转
,将线段AB绕点A按逆时针方向旋转![]() 得到线段AD,其中
得到线段AD,其中![]() 连结BD,CD,
连结BD,CD,![]() .
.
![]() 若
若![]() ,
,![]() ,在图1中补全图形,并写出m值.
,在图1中补全图形,并写出m值.
![]() 如图2,当
如图2,当![]() 为钝角,
为钝角,![]() 时,m值是否发生改变?证明你的猜想.
时,m值是否发生改变?证明你的猜想.
![]() 如图3,
如图3,![]() ,
,![]() ,BD与AC相交于点O,求
,BD与AC相交于点O,求![]() 与
与![]() 的面积比.
的面积比.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:
①2a+b=0;②4a﹣2b+c<0;③ac>0;④当y<0时,x<﹣1或x>2.
其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
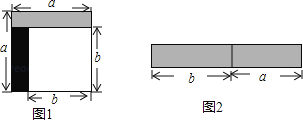
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A、a2﹣2ab+b2=(a﹣b)2 B、a2﹣b2=(a+b)(a﹣b) C、a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下题:
计算:(1﹣![]() )(1﹣
)(1﹣![]() )(1﹣
)(1﹣![]() )…(1﹣
)…(1﹣![]() )(1﹣
)(1﹣![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=110°,则∠1+∠2的度数为( )

A. 80°; B. 90°; C. 100°; D. 110°;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们来定义一种新运算:对于任意实数x、y,“※”为a※b=(a+1)(b+1)﹣1
(1)计算(﹣3)※9
(2)嘉琪研究运算“※”之后认为它满足交换律,你认为她的判断 (正确、错误)
(3)请你帮助嘉琪完成她对运算“※”是否满足结合律的证明.
证明:由已知把原式化简得a※b=(a+1)(b+1)﹣1=ab+a+b
∵(a※b)※c=(ab+a+b)※c=
a※(b※c)=
∴
∴运算“※”满足结合律.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE交AE延长线于D,DM⊥AC交AC的延长线于M,连接CD,以下四个结论:

①∠ADC=45°;②BD=![]() AE;③AC+CE=AB;④AC+AB=2AM.其中正确的结论有( )
AE;③AC+CE=AB;④AC+AB=2AM.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某校有一长方形操场,长为x m,宽为y m,为了美化校园环境,学校决定在操场四周修建m m宽的绿化带,负责后勤的王老师让八年级某班学生计算一下剩下操场的面积,可是该班学生计算出了两种结果:一种是(xy-2mx-2my)m2,另一种是(xy-2mx-2my+4m2)m2,并且为此争论不休,作为一名八年级学生,你能运用所学的知识来帮助他们判断对错吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图①,若AB∥CD,点P在AB,CD外部,则有 ∠B=∠BOD,又因为∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB,CD内部,如图②,以上结论是否成立?若成立,请说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论;
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论,求图④中∠A+∠B+∠C+∠D+∠E的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com