
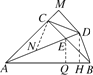
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE交AE延长线于D,DM⊥AC交AC的延长线于M,连接CD,以下四个结论:

①∠ADC=45°;②BD=![]() AE;③AC+CE=AB;④AC+AB=2AM.其中正确的结论有( )
AE;③AC+CE=AB;④AC+AB=2AM.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
①过E作EQ⊥AB于Q.根据角平分线定义和勾股定理及等腰直角三角形性质得AB=AQ+BQ=AC+CE.②作∠ACN=∠BCD,交AD于N.证△ACN≌△BCD(ASA),得CN=CD.根据等腰直角三角形性质得AN=CN,∠NCE=∠AEC=67.5°,CN=NE,CD=AN=EN=![]() AE;③过D作DH⊥AB于H,根据等腰三角形性质和角平分线定义,△DCM≌△DBH(AAS),BH=CM.由勾股定理得AM=AH,所以AC+AB=AC+AH+BH=AC+AM+CM=2AM.
AE;③过D作DH⊥AB于H,根据等腰三角形性质和角平分线定义,△DCM≌△DBH(AAS),BH=CM.由勾股定理得AM=AH,所以AC+AB=AC+AH+BH=AC+AM+CM=2AM.
过E作EQ⊥AB于Q.
∵∠ACB=90°,AE平分∠CAB,
∴CE=EQ.
∵∠ACB=90°,AC=BC,
∴∠CBA=∠CAB=45°.
∵EQ⊥AB,
∴∠EQA=∠EQB=90°.
由勾股定理得AC=AQ,
∴∠QEB=45°=∠CBA,
∴EQ=BQ,
∴AB=AQ+BQ=AC+CE,
∴①③正确;
作∠ACN=∠BCD,交AD于N.
∵∠CAD=![]() ∠CAB=22.5°=∠BAD,
∠CAB=22.5°=∠BAD,
∴∠DBA=90°-22.5°=67.5°,
∴∠DBC=67.5°-45°=22.5°,
∴∠DBC=∠CAD.在△ACN和△BCD中,
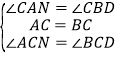
∴△ACN≌△BCD(ASA),CN=CD.
∵∠ACN+∠NCE=90°,
∴∠NCB+∠BCD=90°,
∴∠CND=∠CDN=45°,
∴∠ACN=45°-22.5°=22.5°=∠CAN,
∴AN=CN,
∴∠NCE=∠AEC=67.5°,
∴CN=NE,
∴CD=AN=EN=![]() AE,
AE,
∴②正确;
过D作DH⊥AB于H,
∵∠MCD=∠CAD+∠CDA=67.5°,∠DBA=90°-∠DAB=67.5°,
∴∠MCD=∠DBA.
∵AE平分∠CAB,DM⊥AC,DH⊥AB,
∴DM=DH.在△DCM和△DBH中,
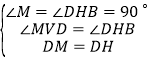
∴△DCM≌△DBH(AAS),
∴BH=CM.
由勾股定理得AM=AH,
∴AC+AB=AC+AH+BH=AC+AM+CM=2AM,
∴④正确.
故选:D


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上. 
(1)连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题“在旋转的过程中,线段DF与BF的长始终相等”是否正确?答: .
(2)若将正方形AEFG绕点A按顺时针方向旋转,连接DG,在旋转过程中,你能否找到一条线段的长与线段DG的长始终相等?并以图为例说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)图2中,当∠D=50度,∠B=40度时,求∠P的度数.
(3)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数轴上有A、B、C三点,且AB=3BC,若B为原点,A点表示数为6.
(1)求C点表示的数;
(2)若数轴上有一动点P,以每秒1个单位的速度从点C向点A匀速运动,设运动时间为t秒,请用含t的代数式表示PB的长;
(3)在(2)的条件下,点P运动的同时有一动点Q从点A以每秒2个单位的速度向点C匀速运动,当P、Q两点相距2个单位长度时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
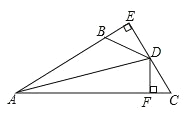
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;(2)已知AC=20, BE=4,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下管道,若由甲队单独铺设,恰好在规定时间内完成;若由乙队单独铺设,需要超过规定时间15天才能完成,如果先由甲、乙两队合做10天,再由乙队单独铺设正好按时完成.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为5000元,乙队每天的施工费用为3000元,为了缩短工期以减少对居民交通的影响,工程指挥部最终决定该工程由甲、乙两队合做来完成,那么该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线为AF,AF与CD交于点E,则△CEF是__________三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF,若将△DEC的边EC沿AC方向移动变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com