
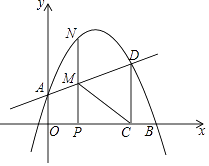
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0),与过A点的直线相交于另一点D(3, ![]() ),过点D作DC⊥x轴,垂足为C.
),过点D作DC⊥x轴,垂足为C.
(1)求抛物线的表达式;
(2)点P在线段OC上(不与点O、C重合),过P作PN⊥x轴,交直线AD于M,交抛物线于点N,连接CM,求△PCM面积的最大值;
(3)若P是x轴正半轴上的一动点,设OP的长为t,是否存在t,使以点M、C、D、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
【答案】
(1)
解:把点B(4,0),点D(3, ![]() ),代入y=ax2+bx+1中得,
),代入y=ax2+bx+1中得, 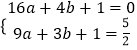 ,
,
解得: 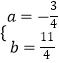 ,
,
∴抛物线的表达式为y=﹣ ![]() x2+
x2+ ![]() x+1
x+1
(2)
解:设直线AD的解析式为y=kx+b,
∵A(0,1),D(3, ![]() ),
),
∴ 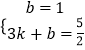 ,
,
∴ ![]() ,
,
∴直线AD的解析式为y= ![]() x+1,
x+1,
设P(t,0),
∴M(t, ![]() t+1),
t+1),
∴PM= ![]() t+1,
t+1,
∵CD⊥x轴,
∴PC=3﹣t,
∴S△PCM= ![]() PCPM=
PCPM= ![]() (3﹣t)(
(3﹣t)( ![]() t+1),
t+1),
∴S△PCM=﹣ ![]() t2+
t2+ ![]() t+
t+ ![]() =﹣
=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
∴△PCM面积的最大值是 ![]()
(3)
解:∵OP=t,
∴点M,N的横坐标为t,
设M(t, ![]() t+1),N(t,﹣
t+1),N(t,﹣ ![]() t2+
t2+ ![]() t+1),
t+1),
∴MN=﹣ ![]() t2+
t2+ ![]() t+1﹣
t+1﹣ ![]() t﹣1=﹣
t﹣1=﹣ ![]() t2+
t2+ ![]() t,CD=
t,CD= ![]() ,
,
如果以点M、C、D、N为顶点的四边形是平行四边形,
∴MN=CD,即﹣ ![]() t2+
t2+ ![]() t=
t= ![]() ,
,
∵△=﹣39,
∴方程﹣ ![]() t2+
t2+ ![]() t=
t= ![]() 无实数根,
无实数根,
∴不存在t,使以点M、C、D、N为顶点的四边形是平行四边形.
【解析】(1)把B(4,0),点D(3, ![]() )代入y=ax2+bx+1即可得出抛物线的解析式;(2)先用含t的代数式表示P、M坐标,再根据三角形的面积公式求出△PCM的面积与t的函数关系式,然后运用配方法可求出△PCM面积的最大值;(3)若四边形BCMN为平行四边形,则有MN=DC,故可得出关于t的二元一次方程,解方程即可得到结论.
)代入y=ax2+bx+1即可得出抛物线的解析式;(2)先用含t的代数式表示P、M坐标,再根据三角形的面积公式求出△PCM的面积与t的函数关系式,然后运用配方法可求出△PCM面积的最大值;(3)若四边形BCMN为平行四边形,则有MN=DC,故可得出关于t的二元一次方程,解方程即可得到结论.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,把一张正方形纸片对折得到长方形ABCD,再沿∠ADC的平分线DE折叠,如图2,点C落在点C′处,最后按图3所示方式折叠,使点A落在DE的中点A′处,折痕是FG,若原正方形纸片的边长为6cm,则FG=cm. 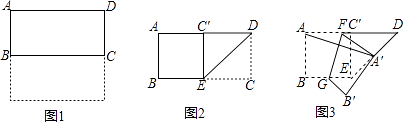
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解七年级男生体质健康情况,随机抽取若干名男生进行测试,测试结果分为优秀、良好、合格、不合格四个等级,统计整理数据并绘制图1、图2两幅不完整的统计图,请根据图中信息回答下列问题:
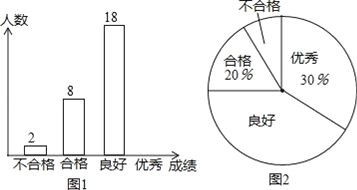
(1)本次接收随机抽样调查的男生人数为 人,扇形统计图中“良好”所对应的圆心角的度数为 ;
(2)补全条形统计图中“优秀”的空缺部分;
(3)若该校七年级共有男生480人,请估计全年级男生体质健康状况达到“良好”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月,某大型商业集团随机抽取所属的部分商业连锁店进行评估,将抽取的各商业连锁店按照评估成绩分成了A、B、C、D四个等级,并绘制了如图不完整的扇形统计图和条形统计图. 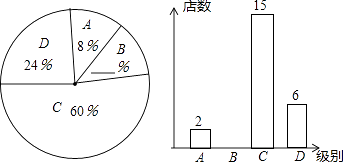
根据以上信息,解答下列问题:
(1)本次评估随即抽取了多少甲商业连锁店?
(2)请补充完整扇形统计图和条形统计图,并在图中标注相应数据;
(3)从A、B两个等级的商业连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及S四边形ABDC.
(2)在y轴上是否存在一点Q,连接QA,QB,使S△QAB=S四边形ABDC?若存在这样一点,求出点Q的坐标;若不存在,试说明理由.
(3)如图②,点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合),给出下列结论:①![]() 的值不变,②
的值不变,②![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数 y=2x 与 y=ax+5 的图象相交于点 A(m,4).
(1)求 A 点坐标及一次函数 y=ax+5 的解析式;
(2)设直线 y=ax+5 与 x 轴交于点 B,求△AOB 的面积;
(3)求不等式 2x<ax+5 的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汶川地震牵动着全国亿万人民的心,某校为地震灾区开展了“献出我们的爱” 赈灾捐款活动.八年级(1)班50名同学积极参加了这次赈灾捐款活动,下表是小明对全班捐款情况的统计表:
捐款(元) | 10 | 15 | 30 |
| 50 | 60 |
人数 | 3 | 6 | 11 |
| 13 | 6 |
因不慎两处被墨水污染,已无法看清,但已知全班平均每人捐款38元.
(1)根据以上信息请帮助小明计算出被污染处的数据,并写出解答过程.
(2)该班捐款金额的众数、中位数分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
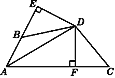
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的数量关系并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和反射出的光线与平面镜所夹的角相等.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射出去,若b镜反射出的光线n平行于m,且∠1=30![]() ,则∠2= ,∠3= ;
,则∠2= ,∠3= ;
(2)在(1)中,若∠1=70![]() ,则∠3= ;若∠1=a,则∠3= ;
,则∠3= ;若∠1=a,则∠3= ;
(3)由(1)(2)请你猜想:当∠3= 时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的?请说明理由.
(提示:三角形的内角和等于180![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com