【题目】如图，已知 
ABC，以AB为直径的圆O分别交AC于D，交BC于E，连接ED，若ED=EC．
求证：AB=AC．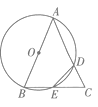
【答案】证明：∵ 
，
∴ 
∵四边形ABED内接于圆，
∴∠B+∠EDA=180°
∵ 
，
∴ 
，
∴ 
,
∴ 
【解析】根据等边对等角得出 ∠ E D C = ∠ C，根据圆的内接四边形的对角互补得出∠B+∠EDA=180°，根据邻补角的定义得出∠ E D C + ∠ E D A = 180 ° ，根据同角的补角相等得出 ∠ B = ∠ E D C ，从而得出 ∠ B = ∠ C ,根据等角对等边得出A B = A C。
【考点精析】通过灵活运用余角和补角的特征和圆内接四边形的性质，掌握互余、互补是指两个角的数量关系，与两个角的位置无关；把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形即可以解答此题．
科目：初中数学 来源： 题型：
【题目】一方有难八方支援，某市政府筹集了抗旱必需物资120吨打算运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：(假设每辆车均满载)
（1）若全部物资都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？
（2）为了节约运费，该市政府可以调用甲、乙、丙三种车型参与运送，已知它们的总辆数为 16辆，你能通过列方程组的方法分别求出几种车型的辆数吗？
（3）求出哪种方案的运费最省？最省是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
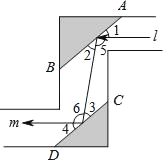
【题目】如图是潜望镜工作原理示意图，阴影部分是平行放置在潜望镜里的两面镜子．已知光线经过镜子反射时，有∠1＝∠2，∠3＝∠4，请解释进入潜望镜的光线l为什么和离开潜望镜的光线m是平行的？
请把下列解题过程补充完整．
理由：
因为AB∥CD，
根据“ ”，
所以∠2＝∠3．
因为∠1＝∠2，∠3＝∠4，
所以∠1＝∠2＝∠3＝∠4，
所以180°﹣∠1﹣∠2＝180°﹣∠3﹣∠4，
即： ．
根据“ ”，
所以l∥m．
查看答案和解析>>
科目：初中数学 来源： 题型：
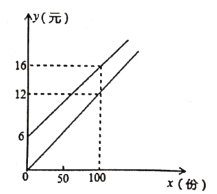
【题目】我校准备实行学案式教学，需印刷若干份数学学案，印刷厂有甲、乙两种收费方式，除按印数收取印刷费外，甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用
（元）与印刷份数
（份）之间的关系如图所式．
（1）求出甲、乙两种收费方式的函数关系式；
（2）我校八年级每次需印刷100-450（含100和450）份学案，选择哪种印刷方式较合算．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,△ABC和△A'B'C'关于直线MN对称,△A'B'C'和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹锐角∠α的数量关系.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】完成下面证明：
（1）如图1，已知直线b∥c，a⊥c，求证：a⊥b.
证明：∵a⊥c （已知）
∴∠1= （垂直定义）
∵b∥c （已知）
∴∠1=∠2 （ ）
∴∠2=∠1=90° （ ）
∴a⊥b （ ）
（2）如图2：AB∥CD，∠B+∠D=180°，求证：CB∥DE．
证明：∵AB∥CD （已知）
∴∠B= （ ）
∵∠B+∠D=180° （已知）
∴∠C+∠D=180° （ ）
∴CB∥DE （ ）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
