
【题目】下列方程中,解是x=﹣![]() 的是( )
的是( )
A. 3(x-![]() )=0 B. 2x﹣(x+1)=0 C.
)=0 B. 2x﹣(x+1)=0 C. ![]() D.
D. ![]()
【答案】C
【解析】
本题考查的是一元一次方程的解的定义,解决本题的方法可以采用代入验证求解,也可以分别求出已知方程的解进行判断,方程的解是指使方程左右两边相等的未知数的值。例如本题就是将x=﹣![]() 依次代入各个方程进行验证,从而得到本题的答案。
依次代入各个方程进行验证,从而得到本题的答案。
答案:C.
把x=﹣![]() 代入选项A. 3(x-
代入选项A. 3(x-![]() )=0,左边=3×(-
)=0,左边=3×(-![]() -
- ![]() )=3×(-1)=-3,右边=0,左边≠右边,所以x=﹣
)=3×(-1)=-3,右边=0,左边≠右边,所以x=﹣![]() 不是已知方程的解;
不是已知方程的解;
把x=﹣![]() 代入选项B. 2x﹣(x+1)=0,左边=2×(﹣
代入选项B. 2x﹣(x+1)=0,左边=2×(﹣![]() )-(﹣
)-(﹣![]() +1)=-1﹣
+1)=-1﹣![]() = -1
= -1![]() ,右边=0,左边≠右边,所以x=﹣
,右边=0,左边≠右边,所以x=﹣![]() 不是已知方程的解;
不是已知方程的解;
把x=﹣![]() 代入选项C.
代入选项C.![]() ,左边=(﹣
,左边=(﹣![]() – 1)×
– 1)×![]() =-
=-![]() ,右边= -
,右边= -![]() ,左边=右边,所以x=﹣
,左边=右边,所以x=﹣![]() 是已知方程的解;
是已知方程的解;
把x=﹣![]() 代入选项D.
代入选项D. ![]() ,左边=
,左边= ![]() ×(﹣
×(﹣![]() )= -
)= -![]() ,右边=0,左边≠右边,所以x=﹣
,右边=0,左边≠右边,所以x=﹣![]() 不是已知方程的解.
不是已知方程的解.
故选C.


科目:初中数学 来源: 题型:
【题目】我们知道,![]() 可以理解为
可以理解为![]() ,它表示:数轴上表示数a的点到原点的距离,这是绝对值的几何意义。进一步地,数轴上的两个点A,B分别用数
,它表示:数轴上表示数a的点到原点的距离,这是绝对值的几何意义。进一步地,数轴上的两个点A,B分别用数![]() 表示,那么A,B两点之间的距离为
表示,那么A,B两点之间的距离为![]() ,反过来,式子
,反过来,式子![]() 的几何意义是:数轴上表示数
的几何意义是:数轴上表示数![]() 的点和表示数
的点和表示数![]() 的点之间的距离。利用此结论,
的点之间的距离。利用此结论,![]() 的意义就是数轴上表示数
的意义就是数轴上表示数![]() 的点到表示-2和表示3的点的距离之和是5,若
的点到表示-2和表示3的点的距离之和是5,若![]() 是整数,则符合
是整数,则符合![]() 的
的![]() 的个数是( )
的个数是( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣(x﹣h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为﹣5,则h的值为( )
A.3﹣ ![]() 或1+
或1+ ![]()
B.3﹣ ![]() 或3+
或3+ ![]()
C.3+ ![]() 或1﹣
或1﹣ ![]()
D.1﹣ ![]() 或1+
或1+ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b互为相反数,b、C互为倒数,并且m的立方等于它本身
(1)求![]() +ac值;
+ac值;
(2)若a>1,且m<0,S=|2a-3b|-2|b-m|-|b+![]() |,求2a-S的值.
|,求2a-S的值.
(3)若m≠0,试讨论:x为有理数时|x+m|-|x-m|是否存在最大值?若存在,求出这个最大值:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M,N分别是斜边AB,DE的中点,点P为AD的中点,连接AE、BD、MN. 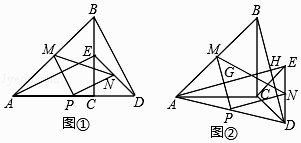
(1)求证:△PMN为等腰直角三角形;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP,BD分别交于点G、H,请判断①中的结论是否成立,若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
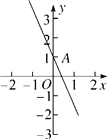
【题目】如图,在平面直角坐标系中,一次函数y=-2x+1的图象与y轴交于点A.
(1)若点A关于x轴的对称点B在一次函数y=![]() x+b的图象上,求b的值,并在同一坐标系中画出该一次函数的图象;
x+b的图象上,求b的值,并在同一坐标系中画出该一次函数的图象;
(2)求这两个一次函数的图象与y轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.
(2)画出△DEF关于直线l对称的三角形.
(3)填空:∠C+∠E= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程x2-2(m+1)x+m2=0.
(1)当m取何值时,方程有两个实数根?
(2)为m选取一个合适的整数,使方程有两个不相等的实数根,并求这两个根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com