
【题目】如图1,在平面直角坐标系中,![]() 为原点,抛物线
为原点,抛物线![]() 经过
经过![]() 三点,且其对称轴为
三点,且其对称轴为![]() 其中点
其中点![]() ,点
,点![]() .
.
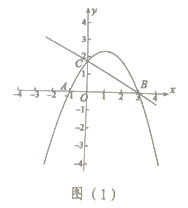
(1)求抛物线的解析式;
(2)①如图(1),点![]() 是直线
是直线![]() 上方抛物线上的动点,当四边形
上方抛物线上的动点,当四边形![]() 的面积取最大值时,求点
的面积取最大值时,求点![]() 的坐标;
的坐标;
②如图(2),连接![]() 在抛物线上有一点
在抛物线上有一点![]() 满足
满足![]() ,请直接写出点
,请直接写出点![]() 的横坐标.
的横坐标.
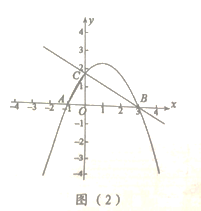
【答案】(1)![]() ;(2)①D
;(2)①D ,②
,②![]() 或
或![]()
【解析】
(1)根据点![]() ,点
,点![]() ,利用待定系数法,可得函数解析式;
,利用待定系数法,可得函数解析式;
(2)①先求出直线BC的解析式,当直线m与抛物线只有一个交点时,点D到BC的距离最远,此时△BCD取最大值,故四边形DCAB有最大值,求出b的值代入原式即可得到答案;
②根据题干条件抛物线上有一点![]() 满足
满足![]() ,通过利用待定系数法利用方程组求出直线BE的解析式,可得答案.
,通过利用待定系数法利用方程组求出直线BE的解析式,可得答案.
解:(1)由题意得:
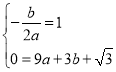
解得![]()
故抛物线的解析式是![]() .
.


图(1) 图(2)
(2)①设直线BC的解析式为y=kx+![]() .
.
∵直线BC过点B(3,0),
∴0=3k+![]()
则k=![]() ,
,
故直线BC解析式为y=![]() x+
x+![]() .
.
设直线m解析式为![]() ,且直线m∥直线BC
,且直线m∥直线BC
当直线m与抛物线只有一个交点时,点D到BC的距离最远,此时△BCD取最大值,故四边形DCAB有最大值.
令![]() ,
,
![]()
当![]() 时
时
直线m与抛物线有唯一交点
解之得:![]()
代入原式可求得:![]()
∴D![]()
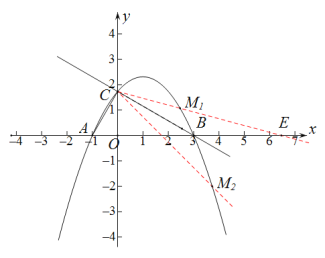
图(3)
过D作DP∥y轴交CB于点P,△DCB面积=△DPC面积+△DPB面积,
∴D
②存在,点M的横坐标为![]() 或
或![]()
解题提示:如图3
符合条件的直线有两条: CM1和CM2(分别在CB的上方和下方)
∵在Rt△ACO中,∠ACO=30°,在Rt△COB中,∠CBO=30°,
∴∠BCM1=∠BCM2=15°
∵△BCE中,∠BCE=∠BEC2=15°
∴BC=BE=![]()
则E(![]() ,0)
,0)
设直线CE解析式为:![]()
∴![]()
解之得:k=![]()
∴直线CE解析式为:![]()
∴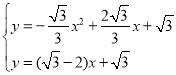
解得:x1=0,x2=2![]() -1
-1
∵ 在Rt△OCF中,∠CBO=30°,∠BCF=15°
∴在Rt△COF中, ∠CFO=45°
∴OC=OF=![]()
∴F(![]() ,0)
,0)
∴直线CF的解析式为![]()
∴
解之得:![]() (舍去),
(舍去),![]()
即点M的横坐标为:![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某地区企业信息化发展水平,从该地区中随机抽取50家企业调研,针对体现企业信息化发展水平的A和B两项指标进行评估,获得了它们的成绩(十分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.A项指标成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
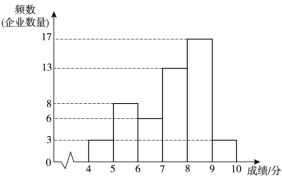
b.A项指标成绩在![]() 这一组的是:
这一组的是:
7.2 7.3 7.5 7.67 7.7 7.71 7.75 7.82 7.86 7.9 7.92 7.93 7.97
c.![]() 两项指标成绩的平均数、中位数、众数如下:
两项指标成绩的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 | |
A项指标成绩 | 7.37 | m | 8.2 |
B项指标成绩 | 7.21 | 7.3 | 8 |
根据以上信息,回答下列问题:
(1)写出表中m的值
(2)在此次调研评估中,某企业A项指标成绩和B项指标成绩都是7.5分,该企业成绩排名更靠前的指标是______________(填“A”或“B”),理由是_____________;
(3)如果该地区有500家企业,估计A项指标成绩超过7.68分的企业数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
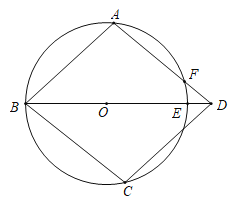
【题目】如图,在⊙O上依次有A、B、C三点,BO的延长线交⊙O于E,![]() ,过点C作CD∥AB交BE的延长线于D,连AD交⊙O于点F.
,过点C作CD∥AB交BE的延长线于D,连AD交⊙O于点F.
(1)求证:四边形ABCD是菱形;
(2)连接OA、OF.
①当∠ABC= °时,点F为![]() 的中点;
的中点;
②若∠AOF=3∠FOE且AF=3,则⊙O的半径是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把某矩形纸片ABCD沿EF、GH折叠(点E、H在AD边上,点F、G在BC边上),使得点B、点C落在AD边上同一点P处,A点的对称点为![]() 点,D点的对称点为
点,D点的对称点为![]() 点,若
点,若![]() ,
,![]() 的面积为4,
的面积为4,![]() 的面积为1,则矩形ABCD的面积等于_____.
的面积为1,则矩形ABCD的面积等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下:
频数分布表
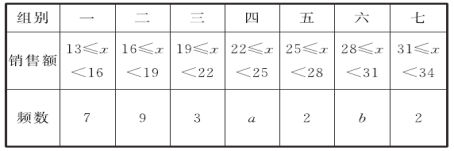
数据分析表
平均数 | 众数 | 中位数 |
20.3 | c | 18 |
请根据以上信息解答下列问题:
(1)填空:a=____,b=_____,c=_____;
(2)若将月销售额不低于25万元确定为销售目标,则有______位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.
(1)甲组抽到A小区的概率是多少;
(2)请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
类别 |
|
|
|
|
|
类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 11 | 20 | 40 |
| 4 |
请你根据以上信息,回答下列问题:
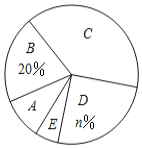
(1)统计表中![]() 的值为_______,统计图中
的值为_______,统计图中![]() 的值为______,
的值为______,![]() 类对应扇形的圆心角为_____度;
类对应扇形的圆心角为_____度;
(2)该校共有1500名学生,根据调查结果,估计该校最喜爱体育节目的学生人数;
(3)样本数据中最喜爱戏曲节目的有4人,其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演,请用树状图或列表求所选2名同学中有男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com