
如图,经过原点的两条直线l1、l2分别与双曲线y= (k≠0)相交于A、B、P、Q四点,其中A、P两点在第一象限,设A点坐标为(3,1).
(k≠0)相交于A、B、P、Q四点,其中A、P两点在第一象限,设A点坐标为(3,1).
(1)求k值及B点坐标;
(2)若P点坐标为(a,3),求a值及四边形APBQ的面积;
(3)若P点坐标为(m,n),且∠APB=90°,求P点坐标.

解答: 解:(1)把A(3,1)代入y=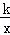 得k=3×1=3,
得k=3×1=3,
∵经过原点的直线l1与双曲线y=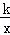 (k≠0)相交于A、B、
(k≠0)相交于A、B、
∴点A与点B关于原点对称,
∴B点坐标为(﹣3,﹣1);
(2)把P(a,3)代入y=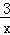 得3a=3,解得a=1,
得3a=3,解得a=1,
∵P点坐标为(1,3),
∵经过原点的直线l2与双曲线y=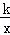 (k≠0)相交于P、Q点,
(k≠0)相交于P、Q点,
∴点P与点Q关于原点对称,
∴点Q的坐标为(﹣1,﹣3),
∵OA=OB,OP=OQ,
∴四边形APBQ为平行四边形,
∵AB2=(3+3)2+(1+1)2=40,PQ2=(1+1)2+(3+3)2=40,
∴AB=PQ,
∴四边形APBQ为矩形,
∵PB2=(1+3)2+(3+1)2=32,PQ2=(3﹣1)2+(1﹣3)2=8,
∴PB=4 ,PQ=2
,PQ=2 ,
,
∴四边形APBQ的面积=PA•PB=2 •4
•4 =16;
=16;
(3)∵四边形APBQ为平行四边形,
而∠APB=90°,
∴四边形APBQ为矩形,
∴OP=OA,
∴m2+n2=32+12=10,
而mn=3,
∵(m+n)2﹣2mn=10,
∴(m+n)2=16,解得m+n=4或m+n=﹣4(舍去),
把m、n看作方程x2﹣4x+3=0的两根,解得m=1,n=3或m=3,n=1(舍去),
∴P点坐标为(1,3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
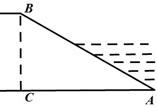 如图所示,河堤横断面迎水坡AB的坡比(指坡面的铅直
如图所示,河堤横断面迎水坡AB的坡比(指坡面的铅直
高度BC与水平宽度CA的比)是1: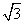 ,堤高BC=5m,
,堤高BC=5m,
则坡面AB的长度是( )
A.10m B.10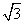 m C.15m D.5
m C.15m D.5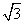 m
m
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,折叠矩形纸片ABCD,使点B落在边AD上,折痕EF的两端分别在AB、BC上(含端点),且AB=6cm,BC=10cm.则折痕EF的最大值是__________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
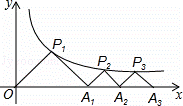
如图所示,P1(x1,y1)、P2(x2,y2),…,Pn(xn,yn)在函数y=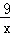 (x>0)的图象上,△OP1A1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An…都是等腰直角三角形,斜边OA1,A1A2,…,An﹣1An,都在x轴上,则y1+y2=__________,y1+y2+…+yn=__________.
(x>0)的图象上,△OP1A1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An…都是等腰直角三角形,斜边OA1,A1A2,…,An﹣1An,都在x轴上,则y1+y2=__________,y1+y2+…+yn=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[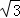 ]=1.现对72进行如下操作:72
]=1.现对72进行如下操作:72 [
[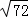 ]=8
]=8 [
[ ]=2
]=2 [
[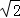 ]=1,这样对72只需进行3次操作后变为1,类似的,①对81只需进行__________次操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是__________.
]=1,这样对72只需进行3次操作后变为1,类似的,①对81只需进行__________次操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
某市广播电视局欲招聘播音员一名,对A、B两名候选人进行了两项素质测试,两人的两项测试成绩如表所示.
 根据实际需要,广播电视局将面试、综合知识测试的得分按3:2的比例计算两人的总成绩,那么__________(填A或B)将被录用.
根据实际需要,广播电视局将面试、综合知识测试的得分按3:2的比例计算两人的总成绩,那么__________(填A或B)将被录用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com