练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．若线段CD是由线段AB平移得到的，点A（-1，3）的对应点为C（2，2），则点B（-3，-1）的对应点D的坐标是（　　）
    A．（0，-2）B．（1，-2）C．（-2，0）D．（4，6）

    分析 根据点A（-1，3）的对应点为C（2，2），可知横坐标由-1变为2，向右移动了3个单位，3变为2，表示向下移动了1个单位，以此规律可得D的对应点的坐标．

    解答 解：点A（-1，3）的对应点为C（2，2），可知横坐标由-1变为2，向右移动了3个单位，3变为2，表示向下移动了1个单位，
    于是B（-3，-1）的对应点D的横坐标为-3+3=0，点D的纵坐标为-1-1=-2，
    故D（0，-2）．
    故选A．

    点评 此题考查了坐标与图形的变化----平移，根据A（-2，3）变为C（3，6）的规律，将点的变化转化为坐标的变化是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．计算：
    （1）（x+a）（x+b）．
    （2）（6m3n）•（-2mn）÷（4mn2）．
    （3）（4x2y-2x3）÷（-2x）2．
    （4）（$\frac{1}{2}$）0×3-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列不等式变形正确的是（　　）
    A．由4x-1≥0得4x＞1B．由3x＞0得x＞-3C．由-2x＜4得x＜-2D．由$\frac{y}{2}$≥0得y≥0

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．定义：如果一个四边形中有一组邻边相等，且这两边夹角的对角被对角线平分，则称这个四边形为准对四边形，这条对角线为准对轴，被等分的角为准对角．如果一个准对四边形的准对角为60°，准对轴长为6，准对轴所对的一个角为120°，则这个四边形的面积为6$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

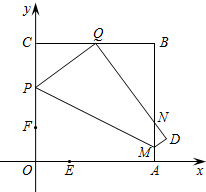    14．如图，四边形OABC为正方形，点A在x轴上，点C在y轴上，点B（8，8），点P在边OC上，点M在边AB上．把四边形OAMP沿PM对折，PM为折痕，使点O落在BC边上的点Q处．动点E从点O出发，沿OA边以每秒1个单位长度的速度向终点A运动，运动时间为t，同时动点F从点O出发，沿OC边以相同的速度向终点C运动，当点E到达点A时，E、F同时停止运动．
    （1）若点Q为线段BC边中点，直接写出点P、M的坐标；
    （2）在（1）的条件下，设△OEF与四边形OAMP重叠面积为S，求S与t的函数关系式；
    （3）在（1）的条件下，在正方形OABC边上是否存在点H，使△PMH为等腰三角形？若存在，求点H的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．已知某几何体的三视图如图所示（单位：cm），则它的侧面展开图的面积是15πcm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．问题提出
    我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，而“作差法”就是常用的解决问题的策略之一．所谓“作差法”：就是通过作差、变形，并利用差的符号确定他们的大小．
    （1）利用“作差法”解决问题
    如图1，把边长为a+b（a≠b）的大正方形分割成两个边长分别是a、b的小正方形及两个矩形，设两个小正方形面积之和为M，两个矩形面积之和为N，试比较M与N的大小．
    （2）类比应用
    ①已知甲、乙两人的速度分别是V甲=$\frac{x+y}{2}$千米/小时、V乙=$\frac{2xy}{x+y}$千米/小时（x、y是正数，且x≠y），试比较V甲、V乙的大小．
    ②如图2，在边长为a的正方形ABCD中，以A为圆心，$\frac{3}{4}a$为半径画弧交AB、AD于点E、F，以CD为直径画弧，若图中阴影部分的面积分别为S1，S2，试比较S1与S2的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．在数轴上A、B两点表示的数分别为-1和$\sqrt{3}$，点B关于点A的对称点为C，则点C表示的数为-2-$\sqrt{3}$；若在此数轴上与点A距离等于5的为点D，则点D表示的数为4或-6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知关于x的分式方程$\frac{x}{x-2}$=$\frac{a}{x-2}$+2无解，求关于y的不等式$\frac{ay-1}{3}$-$\frac{9y+a}{6}$≤1的解集，并在数轴上把解集表示出来．

    查看答案和解析>>

    同步练习册答案