
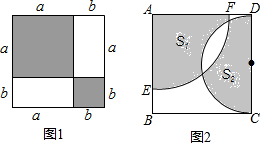
���� ��1����������Ƚ�M��N��С���ɣ�
��2�������üס������˵��ٶ�������������ȫƽ����ʽ���Ƚϼ��ɣ�
�ڷֱ��������������ʾ��S1��S2��ֵ�������Ƚϵó��𰸣�
��� �⣺��1����������ã�M=a2+b2��N=ab+ab��
��M-N=a2+b2-2ab=��a-b��2��0��
��M��N��
��2���١ס������˵��ٶȷֱ���V��=$\frac{x+y}{2}$ǧ��/Сʱ��V��=$\frac{2xy}{x+y}$ǧ��/Сʱ��
��$\frac{x+y}{2}$-$\frac{2xy}{x+y}$=$\frac{��x+y��^{2}}{2��x+y��}$-$\frac{4xy}{2��x+y��}$=$\frac{��x-y��^{2}}{2��x+y��}$��0��
��V����V���Ĵ�С��ϵΪ��V����V����
��������Ӱ���ֵĹ����հ����Ϊd����S1=$\frac{90�У�\frac{3}{4}a��^{2}}{360}$-d=$\frac{9��}{64}$a2-d��
S2=$\frac{180����\frac{a}{2}��^{2}}{360}$-d=$\frac{{��a}^{2}}{16}$-d��
��$\frac{9��}{64}$a2��$\frac{{��a}^{2}}{16}$��
��S1��S2��
���� ������Ҫ�������ı����ۺ��Լ���������ͷ�ʽ�ļӼ������֪ʶ����ȷ��������Ƚ���ʽ��С�ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ȫ��ʵ�� | B�� | ȫ������ | ||
| C�� | n��3 | D�� | ���ڻ����3������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵxOy�У���A������Ϊ��2��0������B�ڵ�һ�����ڣ�OB=AB���ҡ�OBA=45�㣬��P��x���������ϵ�һ���㣨��P�ڵ�A���Ҳࣩ����BPΪ����������BPQ����BP=BQ����PBQ=45�㣮��֪��Q������Ϊ��x��y������y��x�ĺ�����ϵʽ��y=x-2��
��ͼ����ƽ��ֱ������ϵxOy�У���A������Ϊ��2��0������B�ڵ�һ�����ڣ�OB=AB���ҡ�OBA=45�㣬��P��x���������ϵ�һ���㣨��P�ڵ�A���Ҳࣩ����BPΪ����������BPQ����BP=BQ����PBQ=45�㣮��֪��Q������Ϊ��x��y������y��x�ĺ�����ϵʽ��y=x-2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��-2�� | B�� | ��1��-2�� | C�� | ��-2��0�� | D�� | ��4��6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
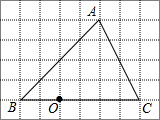 ��ͼ����6��8�������У�ÿ��С�����εı߳���Ϊ1����O�͡�ABC�Ķ����ΪС�����εĶ��㣮
��ͼ����6��8�������У�ÿ��С�����εı߳���Ϊ1����O�͡�ABC�Ķ����ΪС�����εĶ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢ڢ� | B�� | �٢ڢ� | C�� | �ۢܢ� | D�� | �ڢܢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��2 | B�� | 1��0 | C�� | $\frac{1}{3}��-\frac{2}{3}$ | D�� | $-\frac{1}{3}��\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com