
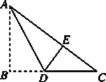
【题目】如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )

A. 6B. 5C. 4D. 3
【答案】D
【解析】
设点B落在AC上的E点处,连接DE,如图所示,由三角形ABC为直角三角形,由AB与BC的长,利用勾股定理求出AC的长,设BD=x,由折叠的性质得到ED=BD=x,AE=AB=6,进而表示出CE与CD,在直角三角形DEC中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出BD的长.
解:∵△ABC为直角三角形,AB=6,BC=8,
∴根据勾股定理得:![]() ,
,
设BD=x,由折叠可知:ED=BD=x,AE=AB=6,
可得:CE=AC-AE=10-6=4,CD=BC-BD=8-x,
在Rt△CDB'中,
根据勾股定理得:(8-x)2=42+x2,
解得:x=3,
则BD=3.
故答案为:3.


科目:初中数学 来源: 题型:
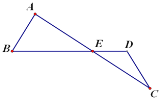
【题目】如图,在△ABE中,∠B=60°,AB=8,C、D分别是△ABE的边AE延长线上和边BE延长线上两点,连接CD,∠A-∠C=60°,AB=CD,DE=6,则线段AC的长度等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
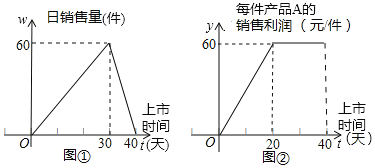
【题目】某商场销售产品A,第一批产品A上市40天内全部售完.该商场对第一批产品A上市后的销售情况进行了跟踪调查,调查结果如图所示:图①中的折线表示日销售量w与上市时间t的关系;图②中的折线表示每件产品A的销售利润y与上市时间t的关系.
(1)观察图①,试写出第一批产品A的日销售量w与上市时间t的关系;
(2)第一批产品A上市后,哪一天这家商店日销售利润Q最大?日销售利润Q最大是多少元?(日销售利润=每件产品A的销售利润×日销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把对角线互相垂直的四边形叫做垂美四边形.
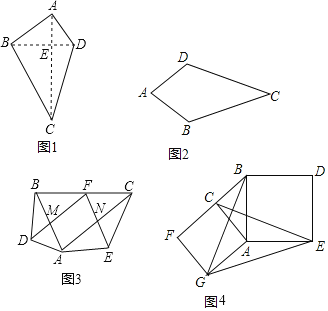
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,那么四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探究:
①如图1,垂美四边形ABCD两组对边AB、CD与BC、AD之间有怎样的数量关系?写出你的猜想,并给出证明.
②如图3,在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在![]() 外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
(3)问题解决:
如图4,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE、BG,GE,已知AC=2,AB=5.求GE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市举行店庆活动,对甲、乙两种商品实行打折销售,打折前,购买2件甲商品和3件乙商品需要180元;购买1件甲商品和4件乙商品需要200元,而店庆期间,购买10件甲商品和10件乙商品仅需520元,这比打折前少花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产![]() 两种产品共60件,需购买甲、乙两种材料.生产一件
两种产品共60件,需购买甲、乙两种材料.生产一件![]() 产品需甲种材料4千克;生产一件
产品需甲种材料4千克;生产一件![]() 产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产![]() 产品不少于38件,问符合生产条件的生产方案有哪几种?
产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件![]() 产品需加工费40元,生产一件
产品需加工费40元,生产一件![]() 产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市对位于笔直公路AC上两个小区A,B的供水路线进行优化改造,供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A,B之间的距离为300(![]() +1)米,求供水站M分别到小区A,B的距离.(结果可保留根号)
+1)米,求供水站M分别到小区A,B的距离.(结果可保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A′________;B′________;C′________;
(2)说明△A′B′C′由△ABC经过怎样的平移得到;
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为________;
(4)求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com