
【题目】已知:2m+2的平方根是±4;3m+n的立方根是﹣1,求:2m﹣n的算术平方根.
【答案】解:因为2m+2的平方根是±4 所以2m+2=(±4)2 , 解得:m=7.
因为3m+n的立方根是﹣1
所以3m+n=(﹣1)3 , 解得:n=﹣22.
所以 ![]() =
= ![]() =
= ![]() =6.
=6.
所以2m﹣n的算术平方根是6
【解析】依据平方根和立方根的定义得到关于m和n的方程,然后再求得代数式2m﹣n的值,最后在求得2m﹣n的算术平方根即可.
【考点精析】认真审题,首先需要了解平方根的基础(如果一个数的平方等于a,那么这个数就叫做a的平方根(或二次方跟);一个数有两个平方根,他们互为相反数;零的平方根是零;负数没有平方根),还要掌握算数平方根(正数a的正的平方根叫做a的算术平方根;正数和零的算术平方根都只有一个,零的算术平方根是零)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】把方程x(x+2)=5(x-2)化成一般式,则a、b、c的值分别是( )
A.1、-3、10
B.1、7、-10
C.1、-5、12
D.1、3、2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中不正确的是( )
A. 平方为9的数是+3或﹣3 B. 立方为27的数是3或﹣3
C. 绝对值为3的数是3或﹣3 D. 倒数等于原数的数是1或﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
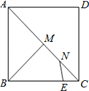
【题目】如图,正方形ABCD的边长为5,点E在边BC上且CE=2,长为![]() 的线段MN在AC上运动,当四边形BMNE的周长最小时,则tan∠MBC的值是( )
的线段MN在AC上运动,当四边形BMNE的周长最小时,则tan∠MBC的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P的坐标为(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是( )
A. (6,-6) B. (1,-1) C. (3,3) D. (6,-6)或(3,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.
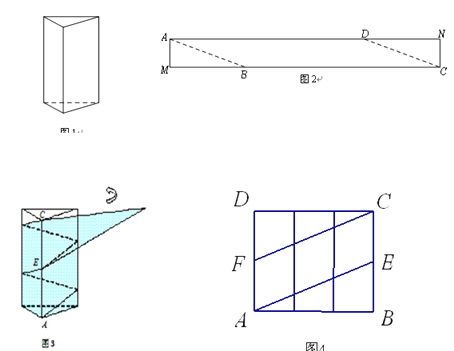
(1)请在图4中画出拼接后符合条件的平行四边形;
(2)请在图2中,计算裁剪的角度(即∠ABM的度数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com