
【题目】如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,D、E为垂足,BD与CE交于点O,则图中全等三角形共有_________对.

 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.对角线互相垂直的平行四边形是正方形
B.一组对边平行另一组对边相等的四边形是平行四边形
C.一组对边平行另一组对角相等的四边形是平行四边形
D.对角线互相垂直的四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
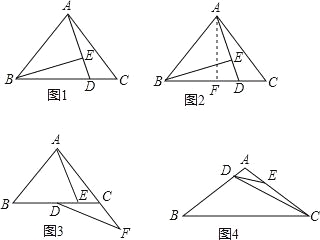
小明遇到这样一个问题:如图1,△ABC中,AB=AC,点D在BC边上,∠DAB=∠ABD,BE⊥AD,垂足为E,求证:BC=2AE.
小明经探究发现,过点A作AF⊥BC,垂足为F,得到∠AFB=∠BEA,从而可证△ABF≌△BAE(如图2),使问题得到解决.
(1)根据阅读材料回答:△ABF与△BAE全等的条件是 AAS(填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个)
参考小明思考问题的方法,解答下列问题:
(2)如图3,△ABC中,AB=AC,∠BAC=90°,D为BC的中点,E为DC的中点,点F在AC的延长线上,且∠CDF=∠EAC,若CF=2,求AB的长;
(3)如图4,△ABC中,AB=AC,∠BAC=120°,点D、E分别在AB、AC边上,且AD=kDB(其中0<k<![]() ),∠AED=∠BCD,求
),∠AED=∠BCD,求![]() 的值(用含k的式子表示).
的值(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列给出的命题中,正确的命题有( )
①等腰三角形的角平分线、中线和高重合;②等腰三角形两腰上的高相等;③等腰三角形最小边是底边;④等边三角形的高、中线、角平分线都相等;⑤等腰三角形都是锐角三角形.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
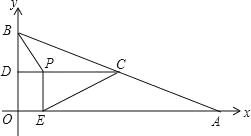
【题目】如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,2),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班预开展社团活动,对全班42名学生开展“你最喜欢的社团”问卷调查(每人只选一项),并将结果制成如下统计表,则学生最喜欢的项目是( )
社团名称 | 篮球 | 足球 | 唱歌 | 器乐 |
人数(人) | 11 | x | 9 | 8 |
A. 篮球B. 足球C. 唱歌D. 器乐
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com