
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=6cm.点P、Q是BC边上两个动点(点Q在点P右边),PQ=2cm,点P从点C出发,沿CB向右运动,运动时间为t秒.5s后点Q到达点B,点P、Q停止运动,过点Q作QD⊥BC交AB于点D,连接AP,设△ACP与△BQD的面积和为S(cm),S与t的函数图像如图2所示.
(1)图1中BC= cm,点P运动的速度为 cm/s;
(2)t为何值时,面积和S最小,并求出最小值;
(3)连接PD,以点P为圆心线段PD的长为半径作⊙P,当⊙P与![]() 的边相切时,求t的值.
的边相切时,求t的值.
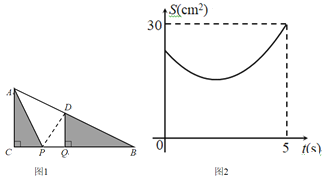
【答案】(1)12 , 2;(2)当t=2时,面积和S最小,最小为21cm2. (3)当t=1或![]() 时⊙P与△ABC的边相切
时⊙P与△ABC的边相切
【解析】
(1)根据题意知,点Q与点B重合时,△ACP的面积为30,依据三角形面积公式可得PC的长为10,由PQ=2得BC的长为12,根据“速度=路程÷时间”可求出点P的速度;
(2)分别求出PC=2t,BQ=10-2t,DQ=5-t,利用三角形面积公式得到二次函数关系式,进行配方即可求出最值;
(3)分⊙P与AB边和AC边相切两种情况进行分类讨论求解即可.
(1)当点Q与点B重合时,△ACP的面积=30,
∴![]()
∵AC=6cm,
∴PC=10cm,
∴BC=PC+PQ=10+2=12cm,
∴点P的速度为:10÷5=2(cm/s);
(2)由题可知PC=2t,BQ=12-2-2t=10-2t,
∵DQ⊥BC,AC⊥BC,
∴DQ∥AC,
∴△DQB∽△ACB,
∴![]() ,即
,即![]()
∴DQ=5-t
∴S=![]() =
=![]()
∴当t=2时,面积和S最小,最小为21cm2.
(3)⊙P与BC边不可能相切
i) ⊙P与AB边相切时△PQD∽△ACB,![]()
∴![]() ,
,
∴t=1
ii)⊙P与AC边相切时![]()
在Rt△PQD中,![]() ,
,
∴![]()
∴t=![]() 或t=
或t=![]() (舍去),
(舍去),
综上当t=1或![]() 时⊙P与△ABC的边相切.
时⊙P与△ABC的边相切.


科目:初中数学 来源: 题型:
【题目】光明中学为了解学生对食堂工作的满意程度,8年级2班数学兴趣小组在全校甲、乙两个班内进行了调查统计,将调查结果分为不满意、一般、满意、非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.


请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数;
(2)求此次调查中结果为非常满意的人数;
(3)兴趣小组准备从调查结果为一般的4位同学中随机选择2位进行回访,已知4位同学中有2位来自甲班,另2位来自乙班,请用列表或用画树状图的方法求出选择的同学均来自甲班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中我们经历了“确定函数的表达,利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程,在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.已知函数y=2![]() ﹣b的定义域为x≥﹣3,且当x=0时y=2
﹣b的定义域为x≥﹣3,且当x=0时y=2![]() ﹣2由此,请根据学习函数的经验,对函数y=2
﹣2由此,请根据学习函数的经验,对函数y=2![]() ﹣b的图象与性质进行如下探究:
﹣b的图象与性质进行如下探究:
(1)函数的解析式为: ;
(2)在给定的平面直角坐标系xOy中,画出该函数的图象并写出该函数的一条性质: ;
(3)结合你所画的函数图象与y=x+1的图象,直接写出不等式2![]() ﹣b≤x+1的解集.
﹣b≤x+1的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(﹣4,1),B(﹣2,3),C(﹣1,2).
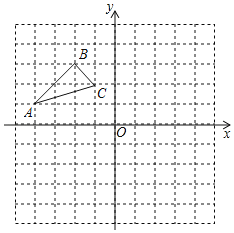
(1)画出△ABC关于原点O成中心对称的△A′B′C′,点A′,B′,C′分别是点A,B,C的对应点.
(2)求过点B′的反比例函数解析式.
(3)判断A′B′的中点P是否在(2)的函数图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校初三学生上周末使用手机的情况(选项:A.聊天;B.学习;C.购物;D.游戏;E.其他),随机抽查了该校初三若干名学生,对其上周末使用手机的情况进行统计(每个学生只选一个选项),绘制了统计表和条形统计图.
选项 | 人数 | 频率 |
A | 15 | 0.3 |
B | 10 | m |
C | 5 | 0.1 |
D | n | |
E | 5 | 0.1 |
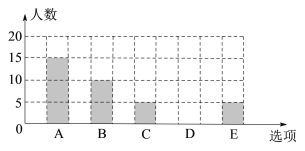
根据以上信息回答下列问题:
(1)这次调查的样本容量是 ;
(2)统计表中m= ,n= ,补全条形统计图;
(3)若该校初三有540名学生,请估计该校初三学生上周末利用手机学习的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船在A处观测灯塔C位于北偏东70o方向上,轮船从A处以每小时30海里的速度沿南偏东50o方向匀速航行,1小时后到达码头B处,此时观测灯塔C位于北偏东25o方向上,求灯塔C与码头B之间的距离(结果保留根号).
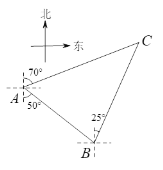
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD,AD=6,AB=8,点P为BC边上的中点,点Q是△ACD的内切圆圆O上的一个动点,点M是CQ的中点,则PM的最大值是( )
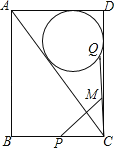
A.![]() ﹣1B.
﹣1B.![]() +1C.3.2D.3
+1C.3.2D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△PAB中,PA=PB,经过A、B作⊙O.

(1)如图1,连接PO,求证:PO平分∠APB;
(2)如图2,点P在⊙O上,PA:AB=![]() :2,E是⊙O上一点,连接AE、BE.求tan∠AEB的值;
:2,E是⊙O上一点,连接AE、BE.求tan∠AEB的值;
(3)如图3,在(2)的条件下,AE经过圆心O,AE交PB于点F,过F作FG⊥BE于点G,EF+BG=14,求线段OF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图象如图所示,则下列结论:
之间,其部分图象如图所示,则下列结论:
![]() ;
;
![]() ;
;
![]() 点
点![]() 、
、![]() 、
、![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;
;
![]() ;
;
![]() (
(![]() 为任意实数).
为任意实数).
其中正确结论的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com