
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,﹣4).
(1)求出图象与x轴的交点A,B的坐标;
(2)在二次函数的图象上是否存在点P,使S△PAB= S△MAB?若存在,求出P点的坐标,若不存在,请说明理由;
S△MAB?若存在,求出P点的坐标,若不存在,请说明理由;
(3)点C在x轴上一动点,以BC为边作正方形BCDE,正方形BCDE还有一个顶点(除点B外)在抛物线上,请写出满足条件的点E的坐标;
(4)将二次函数的图象在x轴下方的部分沿x轴翻折,图象 的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b与此图象至少有三个公共点时,请直接写出b的取值范围是 .
的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b与此图象至少有三个公共点时,请直接写出b的取值范围是 .
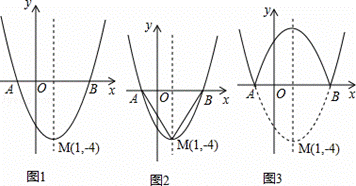
解:(1)∵M(1,﹣4)是二次函数y=(x+m)2+k的顶点坐标,
∴y=(x﹣1)2﹣4=x2﹣2x﹣3,
当 x2﹣2x﹣3=0,解得x1=﹣1,x2=3.
x2﹣2x﹣3=0,解得x1=﹣1,x2=3.
∴A、B两点的坐标 分别为A(﹣1,0),B(3,0);
分别为A(﹣1,0),B(3,0);
(2)在二次函数的图象上存在点P,使
设p(x,y),则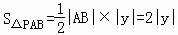 ,又
,又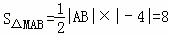 ,
,
∴2|y|=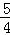 ×8,即y=±5, ∵二次函数的最小值为﹣4, ∴y=5.
×8,即y=±5, ∵二次函数的最小值为﹣4, ∴y=5.
当y=5时,x=﹣2或x=4. ∴P点坐标为(﹣2,5)或(4,5);
(3)不妨设点E在抛物线y=x2﹣ 2x﹣3上,C点的坐标为(m,0).
2x﹣3上,C点的坐标为(m,0).
当BC为正方形BCDE的边时,则E点的坐标为(m,m2﹣2m﹣3).
∵四边形BCDE是正方形,
∴BC=DE, ∴|m﹣3|=|m2﹣2m﹣3|, 即m﹣3=m2﹣2m﹣3,或m﹣3=﹣(m2 ﹣2m﹣3),
﹣2m﹣3),
解得m1=0,m2=3,或m1=﹣2,m2=3,
当m=3时,C点与B点重合,不合题意,舍去,
∴E点的坐标为(0,0)或(﹣2,0),则B1(3,4),B2(3,﹣4),
(4)如图3,依题意知,当﹣1≤x≤3时,翻折后的抛物线的解析式为:y=﹣x2+2x+3
与直线y=x+b与新抛物线有1个交点时,﹣x2+2x+3=x+b,即x2﹣x﹣3﹣b=0,
则△=(﹣1)2﹣4×(﹣3﹣b)=0, 解得 b=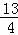
当直线y=x+b经过A(﹣1,0)时﹣1+b=0,可得b=1,
由题意可知y=x+b在y=x+1的下方.由图可知符合题意的b的取值范围1≤b≤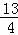 .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
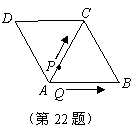
如图所示,菱形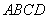 的边长为6厘米,
的边长为6厘米, .从初始时刻开始,点
.从初始时刻开始,点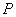 、
、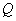 同时从
同时从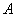 点出发,点
点出发,点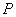 以1厘米/秒的速度沿
以1厘米/秒的速度沿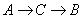 的方向运动,点
的方向运动,点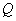 以2厘米/秒的速度沿
以2厘米/秒的速度沿 的方向运动,当点
的方向运动,当点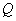 运动到
运动到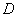 点时,
点时,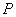 、
、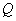 两点同时停止运动,设
两点同时停止运动,设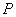 、
、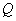 运动的时间为
运动的时间为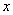 秒时,
秒时,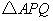 与
与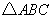 重叠部分的面积为
重叠部分的面积为 平方厘米(这里规定:点和线段是面积为0的三角形),解答下列问题:
平方厘米(这里规定:点和线段是面积为0的三角形),解答下列问题:
(1)点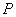 、
、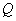 从出发到相遇所用时间是 秒;
从出发到相遇所用时间是 秒;
 (2)点
(2)点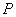 、
、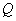 从开始运动到停止的过程中,当
从开始运动到停止的过程中,当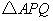 是等边三角形时
是等边三角形时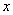
 的值是 秒;
的值是 秒;
( 3)当0≤
3)当0≤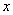 ≤6时,求
≤6时,求 与
与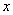 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知△ABC.
(1)用直尺和圆规作出⊙O,使⊙O经过A,C两点,且圆心O在AB边上.(不写作法,保留作图痕迹)
(2)若∠CAB=22.5°,∠B=45°且⊙O的半径为1,
试求出AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
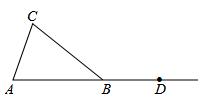
如图,在⊿ABC中,AB=BC,点D在AB的延长线上。
(1)利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)
①作∠CBD的平分线BM ②作边BC上的中线AE,并延长AE交BM于点F
(2)在(1)的基础上,连接CF,判断四边形ABFC的形状,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2014个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是……………………( )
A.(-1,0) B.(1,-2) C.(1,1) D.(-1,-1)
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com