
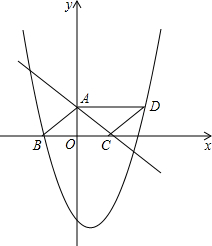
 如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,点B、点D在二次函数y=$\frac{1}{8}$x2+bx+c的图象上,且四边形ABCD是平行四边形.
如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,点B、点D在二次函数y=$\frac{1}{8}$x2+bx+c的图象上,且四边形ABCD是平行四边形.分析 (1)先根据直线与坐标轴相交求出A、C坐标,再根据△ABC是以BC为底边的等腰三角形求出B点坐标,接着ABCD是平行四边形,求出D点坐标;
(2)将B、D坐标代入二次函数解析式即可求出b、c,进而确定二次函数解析式;
(3)用t表示出AP、CQ、AQ,利用PQ⊥AC时△AOC与△PQA,列出比例关系,解出t.
解答 解:(1)∵点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,
∴A(0,3),C(4,0),
∵△ABC是等腰三角形,AB=AC,
∴B(-4,0),
∵ABCD是平行四边形,
∴D(8,3);
(2)将B、D的坐标代入二次函数y=$\frac{1}{8}$x2+bx+c可得:$\left\{\begin{array}{l}{0=2-4b+c}\\{3=8+8b+c}\end{array}\right.$,
解得:b=-$\frac{1}{4}$,c=3,
∴$y=\frac{1}{8}{x}^{2}-\frac{1}{4}x+3$.
(3)
∵AO=3,CO=4,
∴AC=5,
当PQ⊥AC时,如图,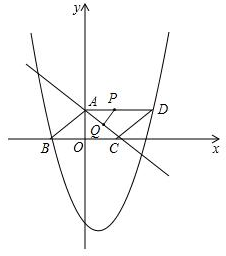
AP=CQ=t,AQ=5-t,
$\frac{AQ}{AP}=\frac{OC}{AC}=\frac{4}{5}$,
∴$\frac{5-t}{t}=\frac{4}{5}$,
解得:$t=\frac{25}{9}$.
即:t为$\frac{25}{9}$时PQ⊥AC.
点评 本题考查了等腰三角形与平行四边形的简单性质、待定系数法求二次函数解析式、相似三角形判定与生质等多个知识点,难度不大,是一道基础题.对于第(3)问,动点的特殊状态的存在性问题,其关键是根据所给特定状态(本题的特定状态就是PQ与AC垂直)找到几何等量关系(本题的几何等量关系就是相似三角形的线段比例关系),利用方程思想解决问题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
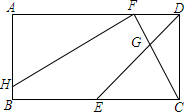 在矩形ABCD中,E为BC的中点,连接DE,F为AD上一点,连接CF,交DE于点G,过点F作HF⊥CF于点F,若$\frac{AB}{BC}=\frac{DG}{GE}$=$\frac{1}{2}$,DF=2.
在矩形ABCD中,E为BC的中点,连接DE,F为AD上一点,连接CF,交DE于点G,过点F作HF⊥CF于点F,若$\frac{AB}{BC}=\frac{DG}{GE}$=$\frac{1}{2}$,DF=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
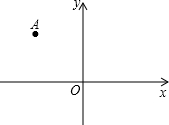 已知抛物线的顶点为坐标原点,且经过点A(-1,1)
已知抛物线的顶点为坐标原点,且经过点A(-1,1)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com