
����Ŀ��ij��˾����һ�ֽ���Ϊ20Ԫ/���ļ���������������y������������ۼ۸�x��Ԫ/�����ı仯���±���
�۸�x��Ԫ/���� | �� | 30 | 40 | 50 | 60 | �� |
������y������� | �� | 5 | 4 | 3 | 2 | �� |
ͬʱ�����۹����е�������֧���������ۣ��ܼ�40��Ԫ��
��1���۲첢�������е�y��x֮��Ķ�Ӧ��ϵ������ѧ����һ�κ�������������������κ������й�֪ʶд��y���������x��Ԫ/�����ĺ�������ʽ��
��2������ù�˾�������ּ������ľ�����z����Ԫ�������ۼ۸�x��Ԫ/�����ĺ�������ʽ�����ۼ۸�Ϊ����Ԫʱ������������ֵ�Ƕ��٣�
��3���ù�˾Ҫ�������ܵ���40��Ԫ����д�����ۼ۸�x��Ԫ/������ȡֵ��Χ�������迼�������������ܴ����ۼ۸�Ӧ��Ϊ����Ԫ��
���𰸡�
��1���⣺���ݱ��������ݿɵó���y��x��һ�κ�����ϵ�������ʽΪ��y=ax+b������ɵã�![]() ��
��
��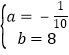 .
.
�ຯ������ʽΪ��y=-![]() x+8.
x+8.
��2���⣺��������ã�z=��x��20��y��40=��x��20���� ![]() x+8����40=
x+8����40= ![]() ��x��50��2+50��
��x��50��2+50��
�� ![]() ��0��
��0��
��x=50��z���=50.
��ù�˾�������ּ������ľ�������z����ʽΪz=-![]() x2 +10x��200�����ۼ۸�Ϊ50Ԫ/��ʱ��������������ֵ��50��Ԫ.
x2 +10x��200�����ۼ۸�Ϊ50Ԫ/��ʱ��������������ֵ��50��Ԫ.
��3���⣺����˾Ҫ������Ϊ40��Ԫʱ���� ![]() (x50)2 +50=40��
(x50)2 +50=40��
��ã�x1=40��x2=60��
������ͼ��IJ�ͼ��ͨ���۲캯��y= ![]() (x50)2 +50��ͼ��֪���չ�˾Ҫ��ʹ����������40��Ԫ�������ۼ۸��ȡֵ��ΧΪ��40��x��60��
(x50)2 +50��ͼ��֪���չ�˾Ҫ��ʹ����������40��Ԫ�������ۼ۸��ȡֵ��ΧΪ��40��x��60��
��y��x�ĺ�����ϵʽΪ��y=-![]() x+8��y��x����������٣����迼�������������ܴ����ۼ۸�Ӧ��Ϊ40Ԫ/��.
x+8��y��x����������٣����迼�������������ܴ����ۼ۸�Ӧ��Ϊ40Ԫ/��.

����������1�����ݱ��������ݿɵó�y��x��һ�κ�����ϵ�������ʽΪ��y=ax+b��������ж�Ԫһ�η����飬��֮���ɵó���.
��2����������=ÿ������������ó�z��x�ĺ�����ϵʽ��z=��x��20��y��40=��x��20���� ![]() x+8����40=
x+8����40= ![]() ��x��50��2+50�����ݺ������ʼ��ɵó���.
��x��50��2+50�����ݺ������ʼ��ɵó���.
��3���ɣ�2���еó��ú�������ʽ����z=40���ⷽ�̼��ɵó����ۼ۸�x1=40��x2=60���迼�������������ܴ����ɺ���ͼ�����ʵó����ۼ۸�Ӧ��Ϊ40Ԫ/��.
�����㾫��������һ�κ��������ʺͶ��κ����������ǽ����ĸ�������Ҫ֪��һ��أ�һ�κ���y=kx+b���������ʣ���1����k>0ʱ��y��x�����������2����k<0ʱ��y��x���������С�������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ2��E�DZ�BC�ϵĶ��㣬BF��AE��CD�ڵ�F������Ϊ��G������CG������˵������AG��GE����AE=BF���۵�G�˶���·����Ϊ�У���CG����Сֵ ![]() ��1��������ȷ��˵���У� ������
��1��������ȷ��˵���У� ������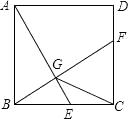
A.4
B.3
C.2
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ��ֱ��L��y��kx+5k��x�Ḻ���ᡢy��������ֱ���A��B���㣮
(1)��OA��OBʱ����ȷ��ֱ��L����ʽ��
(2)��(1)�������£���ͼ����ʾ����QΪAB�ӳ�����һ�㣬����OQ����A��B����ֱ���AM��OQ��M��BN��OQ��N����BN��3����MN�ij���
(3)��Kȡ��ͬ��ֵʱ����B��y�����������˶����ֱ���OB��ABΪ���ڵ�һ���ڶ�����������ֱ�ǡ�OBF�͵���ֱ�ǡ�ABE����EF��y����P�㣬�ʵ���B��y�����˶�ʱ���Բ����ABP������Ƿ�ı䣬�����ı䣬�������ֵ�����ı䣬��˵�����ɣ�
(4)��Kȡ��ͬ��ֵʱ����B��y�����������˶�����ABΪ���ڵڶ�����������ֱ�ǡ�ABE����E��ֱ��______���˶���(ֱ��д��ֱ�ߵı���ʽ)



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ.��֪�������ɶ���ΪT�Ķ��κ��� ![]() ��ͼ����ת45�ȵõ���ֱ��AB��
��ͼ����ת45�ȵõ���ֱ��AB�� ![]() ��������C��D����.
��������C��D����.
��1���߶�AT��Ϊ,
��2����y������һ��P����PC+PD Ϊ��С�����P������Ϊ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����B��E�ֱ���AC��DF�ϣ�BD��CE����AF�ཻ����1����2����C����D����֤����A����F��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ���ϣ�����ʦ�ó�һ����ͼ 1 ��ʾ�ij�����![]() ֽ���Ա�
ֽ���Ա�![]() ���ĸ��Ƕ���ֱ�ǣ��� Ҫ��ͬѧ����ֱ�ߺ��������� AB ������һ�� E��ʹ
���ĸ��Ƕ���ֱ�ǣ��� Ҫ��ͬѧ����ֱ�ߺ��������� AB ������һ�� E��ʹ![]() ��
��

��1����ͬѧ����������![]() ������ȡһ��
������ȡһ��![]() ����
����![]() Ϊ���㣬��
Ϊ���㣬��![]() Ϊһ�ߣ�����������
Ϊһ�ߣ�����������![]() �ǣ�ʹ����һ�߾����� C����
�ǣ�ʹ����һ�߾����� C����![]() ��Ϊ����
������
��2����ͬѧ����������![]() Ϊʼ�ߣ��ڳ����ε��ڲ���������������
Ϊʼ�ߣ��ڳ����ε��ڲ���������������![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ������ͼ 2 ��ʾ
������ͼ 2 ��ʾ![]() ��Ϊ����
������
��֧��_______ͬѧ����������ͼ������__________________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����д�������ɣ�
��ͼ��CD��EF����1=��2����֤����3=��ACB��
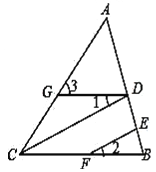
֤������CD��EF��
���DCB=��2����������������������������
�ߡ�1=��2��
���DCB=��1������������ ����������
��GD��CB�������������� ������
���3=��ACB������������ ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����Rt��ABC��Rt��ADE�У���BAC��90������DAE��90����AB��AC��AD��AE��CE��BD�ཻ�ڵ�M��BD��AC���ڵ�N���Բ���BD��CE�кι�ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1����2�������������У�����ʹ��ABC�ա�DBC�������ǡ���������

A. AB��CD B. AC��BD C. ��A����D D. ��ABC����DCB
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com