
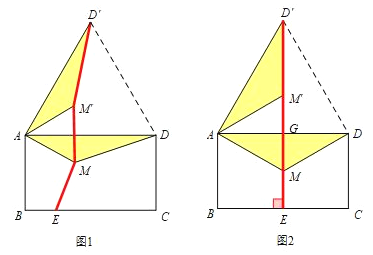
【题目】如图,已知长方形ABCD,AB=1,BC=2,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为( )

A. 1 B. 1+![]() C. 2+
C. 2+![]() D. 3
D. 3
【答案】B
【解析】
将△AMD绕点A逆时针旋转60°得到△AM’D’,MD=M’D’,易得到△ADD’和△AMM’均为等边三角形,推出AM=MM’可得MA+MD+ME=D’M+MM’+ME,共线时最短;由于点E也为动点,可得当D’E⊥BC时最短,此时易求得D’E=DG+GE的值.
将△AMD绕点A逆时针旋转60°得到△AM’D’,MD=M’D’,易得到△ADD’和△AMM’均为等边三角形,
∴AM=MM’,
∴MA+MD+ME=D’M+MM’+ME,
∴D′M、MM′、ME共线时最短,
由于点E也为动点,
∴当D’E⊥BC时最短,此时易求得D’E=DG+GE=4+3![]() ,
,
∴MA+MD+ME的最小值为4+3![]() .
.
故选B.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是( ) 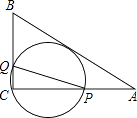
A.4.75
B.4.8
C.5
D.4 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图, 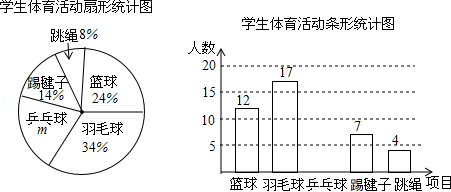
请根据图中提供的信息解答下列各题.
(1)本次问卷调查共抽查了名学生;
(2)请补全条形统计图;
(3)请你估计该校约有名学生最喜爱打篮球;
(4)学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用列表或树状图的方法,求抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
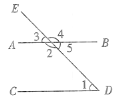
【题目】如图,直线AB,CD被DE所截,则∠1和 是同位角,∠1和 是内错角,∠1和 是同旁内角;
(2)在(1)中,如果∠5=∠1,那么∠1=∠3的推理过程如下,请在括号内注明理由:
因为∠5=∠1( ),
∠5=∠3( ),
所以∠1=∠3( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明解三元一次方程组的消元过程,当他解到第三步时,发现还是无法求出方程组的解,请帮小明分析解题的错因并加以改正.
解方程组: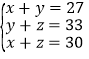
[错解]第一步:①-②,得(消y)x-z=-6④,第二步:②-③,得(消z)y-x=3⑤,第三步:由④⑤组成方程组![]() 此方程组无法求解.
此方程组无法求解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点. 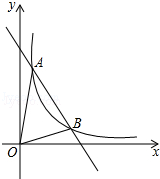
(1)求一次函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(4,0)与y轴交于点C(0,2),抛物线的对称轴交x轴于点D.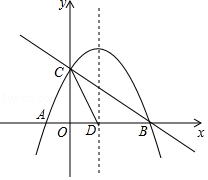
(1)求抛物线的表达式;
(2)在抛物线的对称轴是否存在点P,使△PCD是以CD为腰的等腰三角形,如果存在,求出P点的坐标,若不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?并求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条南北方向的公路上,有一辆出租车停在A地,乘车的第一位客人向南走3千米下车;该车继续向南开,又走了2千米后,上来第二位客人,第二位客人乘车向北走7千米下车,此时恰好有第三位客人上车,先向北走3千米,又调头向南走,结果下车时出租车恰好到了A地.
(1)如果以A地为原点,向北方向为正方向,用1个单位表示1千米,在数轴上表示出第一位客人和第二位客人下车的位置;
(2)第三位客人乘车走了多少千米?
(3)规定出租车的收费标准是4千米内付7元,超过4千米的部分每千米加付1元(不足1千米按1千米算),那么该出租车司机在这三位客人中共收了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是ABCD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )
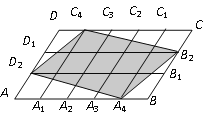
A. 4 B. ![]() C.
C. ![]() D. 30
D. 30
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com