
【题目】甲、乙两大型超市为了吸引顾客,都举行有奖酬宾活动,凡购物满200元,均可得到一次抽奖的机会,在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,抽奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如下表).
甲超市.
球 | 两 红 | 一红一白 | 两 白 |
礼金券(元) | 20 | 50 | 20 |
乙超市:
球 | 两 红 | 一红一白 | 两 白 |
礼金券(元) | 50 | 20 | 50 |
【1】(1)用树状图表示得到一次摸奖机会时中礼金券的所有情况;
【2】(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.
【答案】
【1】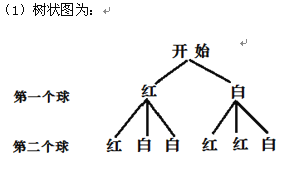
【2】(2)∵去甲超市购物摸一次奖获50元礼金券的概率是P(甲)=![]() =
=![]() ,…………3分
,…………3分
去乙超市购物摸一次奖获50元礼金券的概率是P(乙)=![]() =
=![]() ……………………4分
……………………4分
∴我选择去甲超市购物
【解析】试题分析:(1)让所求的情况数除以总情况数即为所求的概率;
(2)算出相应的平均收益,比较即可.
解:(1)树状图为:
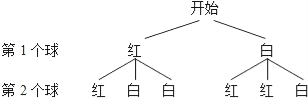
∴一共有6种情况;
(2)方法1:∵去甲超市购物摸一次奖获10元礼金券的概率是P(甲)=![]() ,
,
去乙超市购物摸一次奖获10元礼金券的概率是P(乙)=![]() ,
,
∴我选择去甲超市购物;
方法2:∵两红的概率P=![]() ,两白的概率P=
,两白的概率P=![]() ,一红一白的概率P=
,一红一白的概率P=![]() =
=![]() ,
,
∴在甲商场获礼金券的平均收益是:![]() ×5+
×5+![]() ×10+
×10+![]() ×5=
×5=![]() ;
;
在乙商场获礼金券的平均收益是:![]() ×10+
×10+![]() ×5+
×5+![]() ×10=
×10=![]() .
.
∴我选择到甲商场购物.
说明:树状图表示为如下形式且按此求解第(2)问的,也正确.
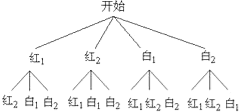


科目:初中数学 来源: 题型:
【题目】大家知道,![]() 它在数轴上表示5的点与原点(即表示0的点)之间的距离.又如式子
它在数轴上表示5的点与原点(即表示0的点)之间的距离.又如式子![]() ,它在数轴上的意义是表示6的点与表示3的点之间的距离.即点A、B在数轴上分别表示数a、b,则A、B两点的距离可表示为:|AB|=
,它在数轴上的意义是表示6的点与表示3的点之间的距离.即点A、B在数轴上分别表示数a、b,则A、B两点的距离可表示为:|AB|=![]() .根据
.根据
以上信息,回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ;数轴上表示-2和-5的两点之间的距离是 .
(2)点A、B在数轴上分别表示实数x和![]() .
.
①用代数式表示A、B两点之间的距;
②如果![]() ,求x的值.
,求x的值.
(3)直接写出代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:
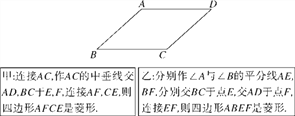
对于甲、乙两人的作法,可判断( )
A. 甲正确,乙错误 B. 甲错误,乙正确
C. 甲、乙均正确 D. 甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:AC为一条直线,O是AC上一点, OE、OF分别平分∠AOB和∠BOC.
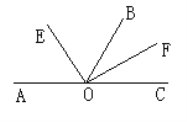
(1)如图:若∠AOB=120°,求∠EOF的大小;
(2)若∠AOB=60°,则∠EOF= _______ °;
(3)任意改变∠AOB的大小,∠EOF的大小会改变吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于两数a和b,给定一种运算 “⊕”: a⊕b=a+b-ab, 则在下列等式中:①a⊕b=b⊕a;②a⊕0=a;③(a⊕b) ⊕c= a⊕(b⊕c) 正确的有___________ (填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为今年将要参加中考的好友小李制作了一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )
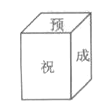
A.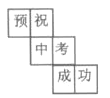 B.
B.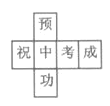 C.
C.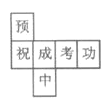 D.
D.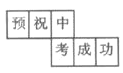
查看答案和解析>>
科目:初中数学 来源: 题型:
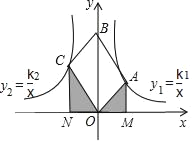
【题目】如图,四边形OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y1=![]() 和y2=
和y2=![]() 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①![]() ②阴影部分面积是
②阴影部分面积是![]() (k1﹣k2)③当∠AOC=90°时,|k1|=|k2|;④若四边形OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是_____.
(k1﹣k2)③当∠AOC=90°时,|k1|=|k2|;④若四边形OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com