练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．如果2x+m=1-x，若m≠-2，那么x的取值范围是x≠1．

    分析 方程整理后，表示出m，根据m≠-2，求出x的范围即可．

    解答 解：方程2x+m=1-x，
    整理得：m=1-3x，
    由m≠-2，得到1-3x≠-2，
    解得：x≠1．
    故答案为：x≠1．

    点评 此题考查了解一元一次方程，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    11．如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”．他们仅仅少走了8步路（假设2步为1米），却踩伤了花草．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．某市规定如下用水收费标准：每户每月用水不超过6立方米时，水费按每立方米a元收费；超过6立方米时，不超过的部分每立方米仍按a元收费，超过的部分每立方米按b元收费．该市某户今年3、4月份的用水量和水费如下表所示：
    月份用水量（立方米）水费（元）
    357.5
    4927
    （1）求出a与b的值；
    （2）求当用户用水为x立方米时的水费（用含x的代数式表示）；
    （3）某用户某月交水费39元，这个月该用户用水多少立方米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．以40m/s的速度将小球沿与地面成30度角的方向击出时，球的飞行路线是一条抛物线．如果不考虑空气阻力，球的飞行高度h（单位m）与飞行时间t（单位s）之间具有函数关系：h=20t-5t2，那么球从飞出到落地要用的时间是4s．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．（1）先化简再求值：（$\frac{a-2}{{a}^{2}+2a}-\frac{a-1}{{a}^{2}+4a+4}$）÷$\frac{a-4}{a+2}$，其中a满足a2+2a-1=0．
    （2）解方程：$\frac{1}{x-3}=\frac{1-x}{3-x}-2$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．一学生扔实心球，实心球行进的高度y（m）与水平距离x（m）的函数表达式为y=-$\frac{1}{5}$x2+$\frac{7}{5}$x+$\frac{8}{5}$，则实心球落地时的水平距离是（　　）
    A．1mB．8mC．9mD．10m

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．中央电视台《为您服务》节目曾播放过骗子骗小学生钱的事件，骗子打着“开发智力的速算法”招牌对学生进行口算演示：
    41×49=2009   82×88=7216   73×77=5621   72×78=5616
    34×36=1224   65×65=4225   56×54=3024   55×55=3025
    学生觉得这种计算方法真简单，比用计算器、还要算的快．这时骗子开始推销一种《速算法》的小册子，高喊：“要得发不离八，每本二十一块八．”小学生纷纷购买，其中一位小学生向他的邻居、七年级学生小刚宣传他得到的速算法，小刚告诉他这种方法只适合两个两位数乘法，并没有宣传的那么神通广大．
    （1）请你再举出两个类似上述运算式子的例子，并总结这些式子中左边两个两位数的特征．你知道小学生向小刚宣传他得到的速算法有怎样一种简便计算的规律？用自己的话叙述出来．
    （2）现在学习了“字母表示数”，你能用字母表示数的方法，直接写出宣传的这种速算法吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图．△ABC是等边三角形．BD是AC边上的中线，E是B、C边上一点（不与B、c重合）
    （1）如图1，若等边三角形ABC的边长为4，若DE⊥BC，连接AE，求AE的长；
    （2）如图2，若DE平分∠BDC，求证：BE=$\sqrt{3}$CE；
    （3）如图3，连接AE，交BD于点M．以AM为边作等边△AMN，连接BN．求证：∠CAE+∠CBD=∠MBN．

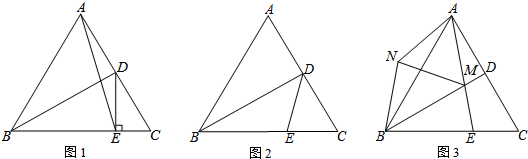
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．计算：（xy2）2÷xy3=xy．

    查看答案和解析>>

    同步练习册答案