
分析 (1)观察题目中的各组数据,可以得到这种简便计算的规律,然后将这种简便的规律写出来即可;
(2)根据第一问的规律写出相应的代数式,然后进行代数式的相乘化简即可解答本题.
解答 解:(1)52×58=3016,28×22=616;
这种简便计算的规律是:十位数字相同,个位数字之和为10的两个两位数数相乘,所得的结果的前两位是原来两个两位数的十位数字与十位数字加1的乘积(如果乘积小于10,就直接把这个数字写下来即可),后两位是原来两个两位数的个位数字的乘积(如果乘积小于10,十位数字用0补齐);
(2)设相乘的两个两位数的十位数字为n,个位数字分别为:m,10-m,
(10n+m)(10n+10-m)
=100n2+100n-10mn+10mn+10m-m2
=100(n2+n)+m(10-m)
=100n(n+1)+m(10-m).
点评 本题考查列代数式和数字的变化类,解题的关键是能观察出题目中数据的变化规律,利用数学归纳法总结出其规律,并用代数式可以推导验证.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
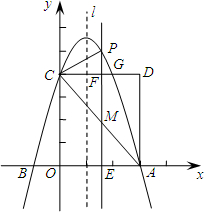 如图,抛物线y=ax2-2ax+c(a≠0)交x轴于A、B两点,A点的坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
如图,抛物线y=ax2-2ax+c(a≠0)交x轴于A、B两点,A点的坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com