
 ČēĶ¼£¬Å×ĪļĻßy=ax2-2ax+c£Øa”Ł0£©½»xÖįÓŚA”¢BĮ½µć£¬AµćµÄ×ų±źĪŖ£Ø3£¬0£©£¬ÓėyÖį½»ÓŚµćC£Ø0£¬4£©£¬ŅŌOC”¢OAĪŖ±ß×÷¾ŲŠĪOADC½»Å×ĪļĻßÓŚµćG£®
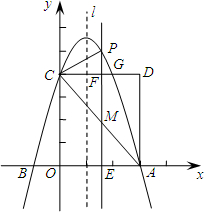
ČēĶ¼£¬Å×ĪļĻßy=ax2-2ax+c£Øa”Ł0£©½»xÖįÓŚA”¢BĮ½µć£¬AµćµÄ×ų±źĪŖ£Ø3£¬0£©£¬ÓėyÖį½»ÓŚµćC£Ø0£¬4£©£¬ŅŌOC”¢OAĪŖ±ß×÷¾ŲŠĪOADC½»Å×ĪļĻßÓŚµćG£®·ÖĪö £Ø1£©½«A£Ø3£¬0£©£¬C£Ø0£¬4£©“śČėy=ax2-2ax+c£¬ŌĖÓĆ“ż¶ØĻµŹż·Ø¼“æÉĒó³öÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ĻČøł¾ŻA”¢CµÄ×ų±ź£¬ÓĆ“ż¶ØĻµŹż·ØĒó³öÖ±ĻßACµÄ½āĪöŹ½£¬½ų¶ųøł¾ŻÅ×ĪļĻßŗĶÖ±ĻßACµÄ½āĪöŹ½·Ö±š±ķŹ¾³öµćP”¢µćMµÄ×ų±ź£¬¼“æɵƵ½PMµÄ³¤£»
£Ø3£©ÓÉÓŚ”ĻPFCŗĶ”ĻAEM¶¼ŹĒÖ±½Ē£¬FŗĶE¶ŌÓ¦£¬ŌņČōŅŌP”¢C”¢FĪŖ¶„µćµÄČż½ĒŠĪŗĶ”÷AEMĻąĖĘŹ±£¬·ÖĮ½ÖÖĒéæö½ųŠŠĢÖĀŪ£ŗ¢Ł”÷PFC”×”÷AEM£¬¢Ś”÷CFP”×”÷AEM£»æÉ·Ö±šÓĆŗ¬mµÄ“śŹżŹ½±ķŹ¾³öAE”¢EM”¢CF”¢PFµÄ³¤£¬øł¾ŻĻąĖĘČż½ĒŠĪ¶ŌÓ¦±ßµÄ±ČĻąµČĮŠ³ö±ČĄżŹ½£¬Ēó³ömµÄÖµ£®
½ā“š ½ā£ŗ£Ø1£©”ßÅ×ĪļĻßy=ax2-2ax+c£Øa”Ł0£©¾¹żµćA£Ø3£¬0£©£¬µćC£Ø0£¬4£©£¬
”ą$\left\{\begin{array}{l}{9a-6a+c=0}\\{c=4}\end{array}\right.$£¬
½āµĆ$\left\{\begin{array}{l}{a=-\frac{4}{3}}\\{c=4}\end{array}\right.$£®
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=-$\frac{4}{3}$x2+$\frac{8}{3}$x+4£»
£Ø2£©ÉčÖ±ĻßACµÄ½āĪöŹ½ĪŖy=kx+b£¬
”ßA£Ø3£¬0£©£¬µćC£Ø0£¬4£©£¬
”ą$\left\{\begin{array}{l}{3k+b=0}\\{b=4}\end{array}\right.$£¬
½āµĆ$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=4}\end{array}\right.$£®
”ąÖ±ĻßACµÄ½āĪöŹ½ĪŖy=-$\frac{4}{3}$x+4£®
”ßµćMµÄŗį×ų±źĪŖm£¬µćMŌŚACÉĻ£¬
”ąMµćµÄ×ų±źĪŖ£Øm£¬-$\frac{4}{3}$m+4£©£¬
”ßµćPµÄŗį×ų±źĪŖm£¬µćPŌŚÅ×ĪļĻßy=-$\frac{4}{3}$x2+$\frac{8}{3}$x+4ÉĻ£¬
”ąµćPµÄ×ų±źĪŖ£Øm£¬-$\frac{4}{3}$m2+$\frac{8}{3}$m+4£©£¬
”ąPM=PE-ME=£Ø-$\frac{4}{3}$m2+$\frac{8}{3}$m+4£©-£Ø-$\frac{4}{3}$m+4£©=-$\frac{4}{3}$m2+4m£¬
¼“PM=-$\frac{4}{3}$m2+4m£Ø0£¼m£¼3£©£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Į¬½įPC£¬ŌŚCDÉĻ·½µÄÅ×ĪļĻß²æ·Ö“ęŌŚÕāŃłµÄµćP£¬Ź¹µĆŅŌP”¢C”¢FĪŖ¶„µćµÄČż½ĒŠĪŗĶ”÷AEMĻąĖĘ£®ĄķÓÉČēĻĀ£ŗ ÓÉĢāŅā£¬æɵĆAE=3-m£¬EM=-$\frac{4}{3}$m+4£¬CF=m£¬ČōŅŌP”¢C”¢FĪŖ¶„µćµÄČż½ĒŠĪŗĶ”÷AEMĻąĖĘ£¬Ēéæö£ŗ
ÓÉĢāŅā£¬æɵĆAE=3-m£¬EM=-$\frac{4}{3}$m+4£¬CF=m£¬ČōŅŌP”¢C”¢FĪŖ¶„µćµÄČż½ĒŠĪŗĶ”÷AEMĻąĖĘ£¬Ēéæö£ŗ
¢ŁPµćŌŚCDÉĻ·½£¬ŌņPF=-$\frac{4}{3}$m2+$\frac{8}{3}$m+4-4=-$\frac{4}{3}$m2+$\frac{8}{3}$m£®
Čō”÷PFC”×”÷AEM£¬ŌņPF£ŗAE=FC£ŗEM£¬
¼“£Ø-$\frac{4}{3}$m2+$\frac{8}{3}$m£©£ŗ£Ø3-m£©=m£ŗ£Ø-$\frac{4}{3}$m+4£©£¬
”ßm”Ł0ĒŅm”Ł3£¬
”ąm=$\frac{23}{16}$£»
¢ŚČō”÷CFP”×”÷AEM£¬ŌņCF£ŗAE=PF£ŗEM£¬
¼“m£ŗ£Ø3-m£©=£Ø-$\frac{4}{3}$m2+$\frac{8}{3}$m£©£ŗ£Ø-$\frac{4}{3}$m+4£©£¬
”ßm”Ł0ĒŅm”Ł3£¬
”ąm=1£®
×ŪÉĻĖłŹö£¬“ęŌŚÕāŃłµÄµćPŹ¹”÷PFCÓė”÷AEMĻąĖĘ£®“ĖŹ±mµÄÖµĪŖ$\frac{23}{16}$»ņ1£®
µćĘĄ “ĖĢāŹĒ¶ž“ĪŗÆŹżµÄ×ŪŗĻĢā£¬½āĢā¹Ų¼üŹĒŹģĮ·ÕĘĪÕ“ż¶ØĻµŹż·ØĒ󶞓ĪŗÆŹż”¢Ņ»“ĪŗÆŹżµÄ½āĪöŹ½£¬¾ŲŠĪµÄŠŌÖŹ£¬ĻąĖĘČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ£¬Ö±½ĒČż½ĒŠĪ”¢µČŃüČż½ĒŠĪµÄÅŠ¶Ø£¬ÄѶȏŹÖŠ£®ŅŖ×¢ŅāµÄŹĒµ±ĻąĖĘČż½ĒŠĪµÄ¶ŌÓ¦±ßŗĶ¶ŌÓ¦½Ē²»Ć÷Č·Ź±£¬ŅŖ·ÖĄąĢÖĀŪ£¬ŅŌĆāĀ©½ā£®


 æĪŹ±ŃµĮ·½ĖÕČĖĆń³ö°ęÉēĻµĮŠ“š°ø
æĪŹ±ŃµĮ·½ĖÕČĖĆń³ö°ęÉēĻµĮŠ“š°ø »ĘøŌ¾µäȤĪ¶æĪĢĆĻµĮŠ“š°ø
»ĘøŌ¾µäȤĪ¶æĪĢĆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | x2-x+1=0 | B£® | x2+2x+2=0 | C£® | £Øx-1£©2+1=0 | D£® | £Øx-1£©£Øx+2£©=0 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
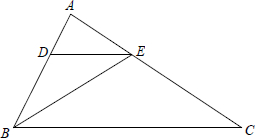 ČēĶ¼”÷ABCÖŠ£¬BEĘ½·Ö”ĻABC£¬DE”ĪBC£¬ČōDE=2AD£¬AE=2£¬ÄĒĆ“EC=4£®
ČēĶ¼”÷ABCÖŠ£¬BEĘ½·Ö”ĻABC£¬DE”ĪBC£¬ČōDE=2AD£¬AE=2£¬ÄĒĆ“EC=4£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com