
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品,需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品,需用甲种原料4千克、乙种原料10千克,可获利润1200元.设生产A种产品的生产件数为x,A、B两种产品所获总利润为y(元).
(1)试写出y与x之间的函数关系式;
(2)求出自变量x的取值范围;
(3)利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少?
【答案】
(1)解:设生产A种产品x件,则生产B种产品(50﹣x)件,
由题意得:y=700x+1200(50﹣x)=﹣500x+60000,
即y与x之间的函数关系式为y=﹣500x+60000
(2)解:由题意得 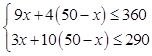 ,
,
解得30≤x≤32.
∵x为整数,
∴整数x=30,31或32
(3)解:∵y=﹣500x+60000,﹣500<0,
∴y随x的增大而减小,
∵x=30,31或32,
∴当x=30时,y有最大值为﹣500×30+60000=45000.
即生产A种产品30件,B种产品20件时,总利润最大,最大利润是45000元
【解析】(1)由于用这两种原料生产A、B两种产品共50件,设生产A种产品x件,那么生产B种产品(50﹣x)件.由A产品每件获利700元,B产品每件获利1200元,根据总利润=700×A种产品数量+1200×B种产品数量即可得到y与x之间的函数关系式;(2)关系式为:A种产品需要甲种原料数量+B种产品需要甲种原料数量≤360;A种产品需要乙种原料数量+B种产品需要乙种原料数量≤290,把相关数值代入得到不等式组,解不等式组即可得到自变量x的取值范围;(3)根据(1)中所求的y与x之间的函数关系式,利用一次函数的增减性和(2)得到的取值范围即可求得最大利润.
【考点精析】掌握一元一次不等式组的应用是解答本题的根本,需要知道1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.


科目:初中数学 来源: 题型:
【题目】如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°,∠C=45°

(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,与过
,与过![]() 点的直线相交于另一点
点的直线相交于另一点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .
.
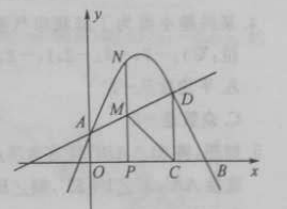
(1)求抛物线的表达式;
(2)点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() 、
、![]() 重合),过
重合),过![]() 作
作![]() 轴,交直线
轴,交直线![]() 于
于![]() ,交抛物线于点
,交抛物线于点![]() ,连接
,连接![]() ,求
,求![]() 面积的最大值;
面积的最大值;
(3)若![]() 是
是![]() 轴正半轴上的一动点,设
轴正半轴上的一动点,设![]() 的长为,是否存在,使以点
的长为,是否存在,使以点![]() 为顶点的四边形是平行四边形?若存在,求出的值;若不存在,请说明理由.
为顶点的四边形是平行四边形?若存在,求出的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个公司有15名工作人员,他们的月工资情况如表.则该公司所有工作人员的月工资的平均数、中位数和众数分别是( )
职务 | 经理 | 副经理 | 职员 |
人数 | 1 | 2 | 12 |
月工资(元) | 5 000 | 2 000 | 800 |
A.520,2 000,2 000
B.2 600,800,800
C.1 240,2 000,800
D.1 240,800,800
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月,某大型商业集团随机抽取所属的部分商业连锁店进行评估,将抽取的各商业连锁店按照评估成绩分成了![]() 、
、![]() 、
、![]() 、
、![]() 四个等级,并绘制了如下不完整的扇形统计图和条形统计图.
四个等级,并绘制了如下不完整的扇形统计图和条形统计图.
根据以上信息,解答下列问题:
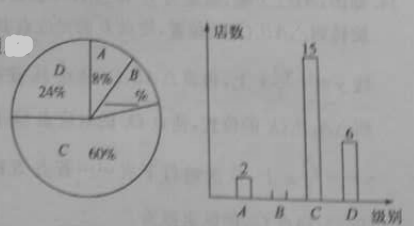
(1)本次评估随机抽取了多少家商业连锁店?
(2)请补充完整扇形统计图和条形统计图,并在图中标注相应数据;
(3)从![]() 、
、![]() 两个等级的商业连锁店中任选2家介绍营销经验,求其中至少有一家是
两个等级的商业连锁店中任选2家介绍营销经验,求其中至少有一家是![]() 等级的概率.
等级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com