
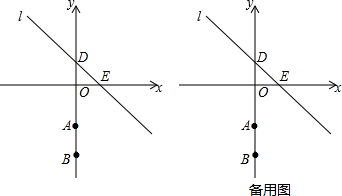
���� ��1������A��ֱ��l����ʱ�����е�ΪM����AM��DE�����ݡ�ADM=45�㣬OD=1�����AD���ٷ������ۣ��������OA�ij����Ӷ����a��
��2������A��AC��l�ڵ�C��ʹAC=AB=2�����ݢٿ�ֱ�ӵó�a������A�ƶ�����D���Ϸ�A�䴦ʱ������B����B��C���l�ڵ�C�䣬ʹB��C=AB=2�������a����������ʹ�á�ABC����ABΪ���ĵ��������Σ����A���߶�AA���ϣ����ɵó�a��ȡֵ��Χ��
��3����ABΪֱ������Q����Q�ڵ�D�·���ʹ��Q��ֱ��l�����ڵ�C�����ACB=90�㣬���ݡ�ODE=45�����DQ�Ӷ��ó���A�������꣬���a������Q�ڵ�D�Ϸ���Q���ʱ������Q����ֱ��l�����ڵ�C�䣬���AC��B=90�㣬ͬ�������A�������꣬���a�������ݡ�Q��Բ���ڵ�Q��Q��֮��ʱ����ACB=90�㣬�������a��ȡֵ��Χ��
��� �⣺��1����A��ֱ��l����ʱ�����е�ΪM������AM����AM��DE��
��ֱ��l�ı���ʽΪy=-x+1��
��D��0��1����E��1��0����
���ADM=45�㣬
���AMD�ǵ���ֱ�������Σ�
��AM=2��
��AD=2$\sqrt{2}$��
�ٵ�A����D���·�ʱ��OA=AD-OD=2$\sqrt{2}$-1����a=1-2$\sqrt{2}$��
�ڵ�A����D���Ϸ�ʱ��OA=OD+AD=2$\sqrt{2}$+1����a=2$\sqrt{2}$+1��
����a=1-2$\sqrt{2}$��2$\sqrt{2}$+1��
��2����ͼ��
����A��AC��l�ڵ�C��ʹAC=AB=2��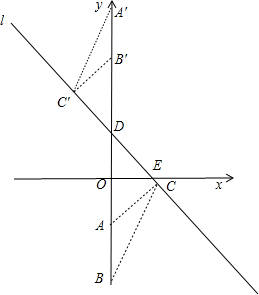
�ɢٵã�a=-2$\sqrt{2}$+1��
����A�ƶ�����D���Ϸ�A�䴦ʱ������B����B��C���l�ڵ�C�䣬ʹB��C��=AB=2��
ͬ���ɵã�B��D=2$\sqrt{2}$��
��a=2$\sqrt{2}$+1+2=2$\sqrt{2}$+3��
����ʹ�á�ABC����ABΪ���ĵ��������Σ����A���߶�AA���ϣ�
��a��ȡֵ��ΧΪ-2$\sqrt{2}$+1��a��2$\sqrt{2}$+3��
�ʴ�Ϊ��-2$\sqrt{2}$+1��a��2$\sqrt{2}$+3��
��3����ABΪֱ������Q����Q�ڵ�D�·���ʹ��Q��ֱ��l�����ڵ�C��
��QC��l��QC=QA=1����ACB=90�㣬
�ߡ�ODE=45�㣬
��DC=QC=1��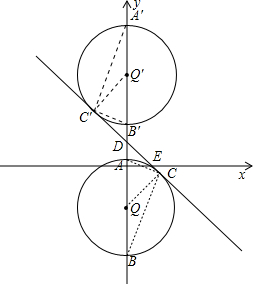
��DQ=$\sqrt{2}$��
��AD=DQ-AQ=$\sqrt{2}$-1��
���A��������Ϊ1-��$\sqrt{2}$-1��=2-$\sqrt{2}$��
��a=2-$\sqrt{2}$��
����Q�ڵ�D�Ϸ���Q���ʱ������Q����ֱ��l�����ڵ�C�䣬
���AC��B=90�㣬ͬ���ɵ�DQ��=$\sqrt{2}$��
��AQ��=1��
��AD=AQ��+DQ��=$\sqrt{2}$+1��
��AO=AD+OD=$\sqrt{2}$+1+1=$\sqrt{2}$+2��
���A��������Ϊ$\sqrt{2}$+2��
��a=$\sqrt{2}$+2��
�ߡ�Q��Բ���ڵ�Q��Q��֮��ʱ����ACB=90�㣬
��a��ȡֵ��ΧΪ2-$\sqrt{2}$��a��2+$\sqrt{2}$��
���� ���⿼����һ�κ����ۺϣ��õ���֪ʶ����һ�κ�����ͼ�������ʡ�Բ�ܽǶ��������ɶ����ȣ��ؼ��Ǹ������⻭��ͼ�Σ�ע�������������ۣ���Ҫ©�⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-3��2������ƽ������-3 | B�� | $\sqrt{225}$��ƽ�����ǡ�15�� | ||
| C�� | ��x=2ʱ��x$\sqrt{x-2}$=0 | D�� | $\frac{\sqrt{3}}{2}$�Ƿ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪���κ�����ͼ��A��3��0����B��0��-3����C��-2��5�����㣮
��֪���κ�����ͼ��A��3��0����B��0��-3����C��-2��5�����㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com