练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点在双曲线上，垂直轴，垂足为，点在上，平行于轴交曲线于点，直线与轴交于点，已知，点的坐标为.

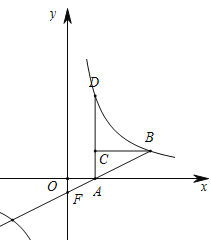
    （1）求该双曲线的解析式；

    （2）求的面积.

    【答案】（1）双曲线解析式为；（2）

    【解析】

    （1）由题意可知点的坐标为得，而，得到，则点坐标为，然后利用待定系数法确定双曲线的解析式；

    （2）根据题意已知和，利用待定系数法确定直线的解析式，得到点的坐标，然后利用三角形的面积公式进行计算即可．

    解：（1）∵点的坐标为，垂直轴，

    ∴，

    又∵，

    ∴，

    ∴点坐标为，

    设双曲线的解析式为，

    把代入得，，

    所以双曲线解析式为；

    （2）设直线的解析式为，

    ∵平行于轴交曲线于点，

    ∵双曲线的解析式为，

    ∴

    ∴把和代入得，，

    解得，，

    ∴线段的解析式为，

    令，得，

    ∴点的坐标为，

    ∴．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，直角三角形ABC中，∠ACB=900，AB=10， BC=6，在线段AB上取一点D，作DF⊥AB交AC于点F.现将△ADF沿DF折叠，使点A落在线段DB上，对应点记为A1；AD的中点E的对应点记为E1.若△E1FA1∽△E1BF，则AD= .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1是实验室中的一种摆动装置，BC在地面上，支架ABC是底边为BC的等腰直角三角形，摆动臂AD可绕点A旋转，摆动臂DM可绕点D旋转，AD＝30，DM＝10．

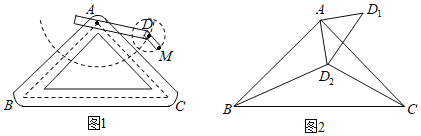
    （1）在旋转过程中，

    ①当A，D，M三点在同一直线上时，求AM的长．

    ②当A，D，M三点为同一直角三角形的顶点时，求AM的长．

    （2）若摆动臂AD顺时针旋转90°，点D的位置由△ABC外的点D1转到其内的点D2处，连结D1D2，如图2，此时∠AD2C＝135°，CD2＝60，求BD2的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

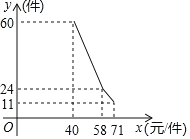
    【题目】某店因为经营不善欠下38000元的无息贷款的债务，想转行经营服装专卖店又缺少资金．“中国梦想秀”栏目组决定借给该店30000元资金，并约定利用经营的利润偿还债务（所有债务均不计利息）已知该店代理的某品牌服装的进价为每件40元，该品牌服装日的售量y（件）与销售价x（元/件）之间的关系可用图中的一条折线（实线）来表示．

    （1）求日销售量y（件）与销售价x（元/件）之间的函数关系式；

    （2）当销售价为多少元时，该店的日销售利润最大；

    （3）该店每天支付工资和其它费用共250元，该店能否在一年内还清所有债务．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着生活水平的提高，人们对饮水品质的需求越来越高，某公司根据市场需求代理A，B两种型号的净水器，其中A型净水器每台的利润为400元，B型净水器每台的利润为500元．该公司计划再一次性购进两种型号的净水器共100台，其中B型净水器的进货量不超过A型净水器的2倍，设购进A型净水器x台，这100台净水器的销售总利润为y元．

    （1）求y关于x的函数关系式；

    （2）该公司购进A型、B型净水器各多少台，才能使销售总利润最大，最大利润是多少？

    （3）实际进货时，厂家对A型净水器出厂价下调a（0＜a＜150）元，且限定公司最多购进A型净水器60台，若公司保持同种净水器的售价不变，请你根据以上信息，设计出使这100台净水器销售总利润最大的进货方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在平面直角坐标系中△ABC三个顶点的坐标分别是点A(﹣2，3)、点B(﹣1，1)、点C(0，2)．

    （1）作△ABC关于C成中心对称的△A1B1C1；

    （2）将△A1B1C1向右平移3个单位，作出平移后的△A2B2C2；

    （3）在x轴上求作一点P，使PA1+PC1的值最小，并写出点 P 的坐标．（不写解答过程，直接写出结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y＝ax2+bx+c的图象交x轴于A(﹣2，0)和点B，交y轴负半轴于点C，且OB＝OC．以下结论：①＞0：②ac＝b﹣1；③4a+c＞0；④b≠2．其中正确的个数有（ ）

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 如图，已知AB=4，P为线段AB上的一个动点，分别以AP，PB为边在AB的同侧作菱形APCD和菱形PBFE，点P，C，E在一条直线上，∠DAP=60°．M，N分别是对角线AC，BE的中点．当点P在线段AB上移动时，点M，N之间的距离最短为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在x轴正半轴上依次截取OA1＝A1A2＝A2A…An﹣1An（n为正整数），过点A1、A2、A3、…、An分别作x轴的垂线，与反比例函数y＝（x＞0）交于点P1、P2、P3、…、Pn，连接P1P2、P2P3、…、Pn﹣1Pn，过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn﹣1An﹣1作垂线段，构成的一系列直角三角形（见图中阴影部分）的面积和是__

    查看答案和解析>>

    同步练习册答案