
科目:初中数学 来源: 题型:
阅读下列材料:
我们知道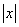 的几何意义是在数轴上数
的几何意义是在数轴上数 对应的点与原点的距离,即
对应的点与原点的距离,即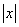 =
= ,也就是说,
,也就是说,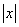 表示在数轴上数
表示在数轴上数 与数0对应的点之间的距离;这个结论可以推广为
与数0对应的点之间的距离;这个结论可以推广为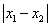 表示在数轴上数
表示在数轴上数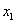 与数
与数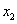 对应的点之间的距离;
对应的点之间的距离;
例1.解方程| |=2.因为在数轴上到原点的距离为2的点对应的数为
|=2.因为在数轴上到原点的距离为2的点对应的数为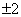 ,所以方程|
,所以方程| |=2的解为
|=2的解为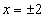 .
.
例2.解不等式| -1|>2.在数轴上找出|
-1|>2.在数轴上找出| -1|=2的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为-1或3,所以方程|
-1|=2的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为-1或3,所以方程| -1|=2的解为
-1|=2的解为 =-1或
=-1或 =3,因此不等式|
=3,因此不等式| -1|>2的解集为
-1|>2的解集为 <-1或
<-1或 >3.
>3.

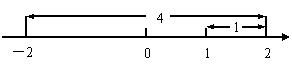 例3.解方程|
例3.解方程| -1|+|
-1|+| +2|=5.由绝对值的几何意义知,该方程就是求在数轴上到1和-2对应的点的距离之和等于5的点对应的
+2|=5.由绝对值的几何意义知,该方程就是求在数轴上到1和-2对应的点的距离之和等于5的点对应的 的值.因为在数轴上1和-2对应的点的距离为3(如图),满足方程的
的值.因为在数轴上1和-2对应的点的距离为3(如图),满足方程的 对应的点在1的右边或-2的左边.若
对应的点在1的右边或-2的左边.若 对应的点在1的右边,可得
对应的点在1的右边,可得 =2;若
=2;若 对应的点在-2的左边,可得
对应的点在-2的左边,可得 =-3,因此方程|
=-3,因此方程| -1|+|
-1|+| +2|=5的解是
+2|=5的解是 =2或
=2或 =-3.
=-3.
参考阅读材料,解答下列问题:
(1)方程| +3|=4的解为 ;
+3|=4的解为 ;
(2)解不等式:| -3|≥5;
-3|≥5;
(3)解不等式:| -3|+|
-3|+| +4|≥9.
+4|≥9.
查看答案和解析>>
科目:初中数学 来源: 题型:
从一块正方形的木板上锯掉2 m宽的长方形木条,剩下的面积是48 m2,则原来这块木板的面积是( )
A.100 m2 B.64 m2
C.121 m2 D.144 m2
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)如图1, 、
、 是正方形
是正方形 的边
的边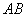 及
及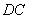 延长线上的点,且
延长线上的点,且
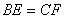 ,则
,则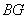 与
与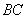 的数量关系是 .
的数量关系是 .
(2)如图2,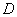 、
、 是等腰
是等腰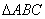 的边
的边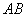 及
及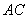 延长线上的点,且
延长线上的点,且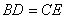 ,连接
,连接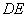 交
交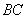 于点
于点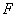 ,
,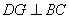 交
交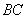 于点
于点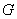 ,试判断
,试判断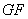 与
与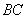 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)如图3,已知矩形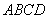 的一条边
的一条边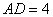 ,将矩形
,将矩形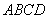 沿过
沿过 的直线折叠,使得顶点
的直线折叠,使得顶点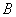 落在
落在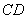 边上的
边上的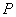 点处。动点
点处。动点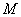 在线段
在线段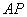 上(点
上(点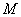 与点
与点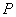 、
、 不重合),动点
不重合),动点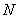
 在线段
在线段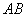 的延长线上,且
的延长线上,且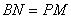 ,连接
,连接 交
交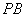 于点
于点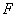 ,作
,作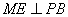 于点
于点 ,且
,且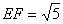 ,试根据上题的结论求出矩形ABCD的面积
,试根据上题的结论求出矩形ABCD的面积


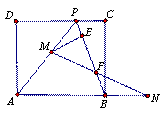
图1 图2 图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com