
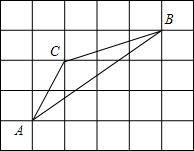
 如图,在正方形网格中每个小正方形的边长均为1,△ABC的各个顶点都在正方形的顶点上,计算sinA,cosA,tanA与sinB,cosB,tanB的值.
如图,在正方形网格中每个小正方形的边长均为1,△ABC的各个顶点都在正方形的顶点上,计算sinA,cosA,tanA与sinB,cosB,tanB的值. 分析 根据正方形网格中每个小正方形的边长均为1,可以求得边AB、AC、BC的长,从而可以求得∠A的余弦值,∠B的余弦值,从而推导出∠A的正弦值和正切值,∠B的正弦值和正切值.
解答 解:∵在正方形网格中每个小正方形的边长均为1,
∴AC=$\sqrt{{1}^{2}+{2}^{2}}=\sqrt{5}$,BC=$\sqrt{{1}^{2}+{3}^{2}}=\sqrt{10}$,AB=$\sqrt{{3}^{2}+{4}^{2}}=\sqrt{25}=5$,
∴cosA=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}=\frac{{5}^{2}+(\sqrt{5})^{2}-(\sqrt{10})^{2}}{2×5×\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
∴sinA=$\sqrt{1-co{s}^{2}A}=\sqrt{1-(\frac{2\sqrt{5}}{5})^{2}}=\frac{\sqrt{5}}{5}$,
∴tanA=$\frac{sinA}{cosA}=\frac{\frac{\sqrt{5}}{5}}{\frac{2\sqrt{5}}{5}}=\frac{1}{2}$,
∴cosB=$\frac{B{C}^{2}+B{A}^{2}-A{C}^{2}}{2BC•BA}=\frac{(\sqrt{10})^{2}+{5}^{2}-(\sqrt{5})^{2}}{2×\sqrt{10}×5}$=$\frac{3\sqrt{10}}{10}$,
∴sinB=$\sqrt{1-co{s}^{2}B}=\sqrt{1-(\frac{3\sqrt{10}}{10})^{2}}=\frac{\sqrt{10}}{10}$,
∴tanB=$\frac{sinB}{cosB}=\frac{\frac{\sqrt{10}}{10}}{\frac{3\sqrt{10}}{10}}=\frac{1}{3}$,
即sinA=$\frac{\sqrt{5}}{5}$,$cosA=\frac{2\sqrt{5}}{5},tanA=\frac{1}{2}$,$sinB=\frac{\sqrt{10}}{10},cosB=\frac{3\sqrt{10}}{10}$,$tanB=\frac{1}{3}$.
点评 本题考查解直角三角形,解题的关键是根据题意求出各边的长,然后求出各角的余弦值.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:解答题
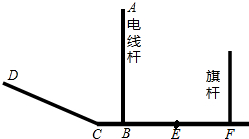 如图,CF为水平面,CD为坡面,线段EF为某一时刻旗杆在太阳光下的影子.
如图,CF为水平面,CD为坡面,线段EF为某一时刻旗杆在太阳光下的影子.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
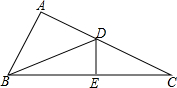 如图所示,△ADB≌△EDB,△BDE≌△CDE,点B,E,C三点在同一直线上,
如图所示,△ADB≌△EDB,△BDE≌△CDE,点B,E,C三点在同一直线上,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com