
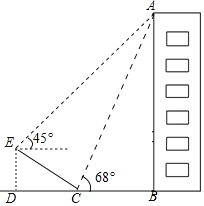
【题目】某学校有一栋教学楼AB,小明(身高忽略不计)在教学楼一侧的斜坡底端C处测得教学楼顶端A的仰角为68°,他沿着斜坡向上行走到达斜坡顶端E处,又测得教学楼顶端A的仰角为45°.已知斜坡的坡角(∠ECD)为30°,坡面长度CE=6m,求楼房AB的高度.(结果精确到0.1m,参考数据:tan68°≈2.48,![]() ≈1.73)
≈1.73)
科目:初中数学 来源: 题型:
【题目】某养殖场计划用96米的竹篱笆围成如图所示的①、②、③三个养殖区域,其中区域①是正方形,区域②和③是矩形,且AG∶BG=3∶2.设BG的长为2x米.
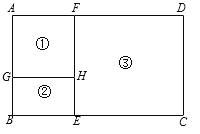
(1)用含x的代数式表示DF= ;
(2)x为何值时,区域③的面积为180平方米;
(3)x为何值时,区域③的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AC与⊙O相切于点A,点B为⊙O上一点,且OC⊥OB于点O,连接AB交OC于点D.
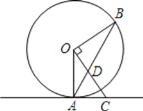
(1)求证:AC=CD;
(2)若AC=3,OB=4,求OD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
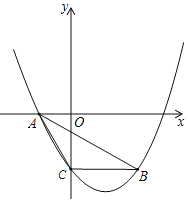
【题目】如图,抛物线y=ax2+bx﹣4经过A(﹣3,0),B(5,﹣4)两点,与y轴交于点C,连接AB,AC,BC.
(1)求抛物线的表达式;
(2)求△ABC的面积;
(3)抛物线的对称轴上是否存在点M,使得△ABM是直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把一条抛物线先向上平移1个单位长度,然后绕原点旋转180°得到抛物线y=x2+5x+6.则原抛物线的顶点坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
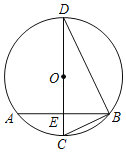
【题目】如图,CD是⊙O的直径,AB是⊙O的弦,CD⊥AB,垂足为E,连接BC、BD.点F为线段CB上一点,连接DF,若CE=2,AB=8,BF=![]() ,则tan∠CDF=__.
,则tan∠CDF=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,抛物线y=![]() ax2+
ax2+![]() ax+
ax+![]() a(a≠0)交x轴于点A和点B(点A在点B左边),交y轴于点C,连接AC,tan∠CAO=3.
a(a≠0)交x轴于点A和点B(点A在点B左边),交y轴于点C,连接AC,tan∠CAO=3.

(1)如图1,求抛物线的解析式;
(2)如图2,D是第一象限的抛物线上一点,连接DB,将线段DB绕点D顺时针旋转90°,得到线段DE(点B与点E为对应点),点E恰好落在y轴上,求点D的坐标;
(3)如图3,在(2)的条件下,过点D作x轴的垂线,垂足为H,点F在第二象限的抛物线上,连接DF交y轴于点G,连接GH,sin∠DGH=![]() ,以DF为边作正方形DFMN,P为FM上一点,连接PN,将△MPN沿PN翻折得到△TPN(点M与点T为对应点),连接DT并延长与NP的延长线交于点K,连接FK,若FK=
,以DF为边作正方形DFMN,P为FM上一点,连接PN,将△MPN沿PN翻折得到△TPN(点M与点T为对应点),连接DT并延长与NP的延长线交于点K,连接FK,若FK=![]() ,求cos∠KDN的值.
,求cos∠KDN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,点C为![]() 的中点,∠ACB=120°,OC的延长线与AD交于点D,且∠D=∠B.
的中点,∠ACB=120°,OC的延长线与AD交于点D,且∠D=∠B.
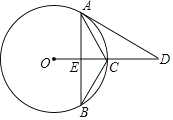
(1)求证:AD与⊙O相切;
(2)若CE=4,求弦AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
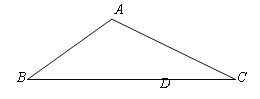
【题目】如图,在△ABC中,AB=3,AC=4,BC=6,D是BC上一点,CD=2,过点D的直线l将△ABC分成两部分,使其所分成的三角形与△ABC相似,若直线l与△ABC另一边的交点为点P,则DP=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com